
科目: 来源: 题型:
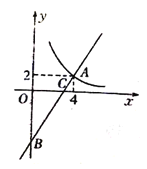
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象在第一象限交于点
的图象在第一象限交于点![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,且
,且![]() .
.
(1)求函数![]() 和
和![]() 的表达式.
的表达式.
(2)已知直线![]() 与
与![]() 轴相交于点
轴相交于点![]() 在第一象限内,求反比例函数
在第一象限内,求反比例函数![]() 的图象上一点
的图象上一点![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目: 来源: 题型:
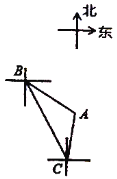
【题目】如图,轮船从![]() 处以每小时60海里的速度沿南偏东
处以每小时60海里的速度沿南偏东![]() 方向匀速航行,在
方向匀速航行,在![]() 处观测灯塔
处观测灯塔![]() 位于南偏东
位于南偏东![]() 方向上,轮船航行40分钟到达
方向上,轮船航行40分钟到达![]() 处,在
处,在![]() 处观测灯塔
处观测灯塔![]() 位于北偏东
位于北偏东![]() 方向上,求
方向上,求![]() 处与灯塔
处与灯塔![]() 的距离.
的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一位篮球运动员在距离篮圈中心水平距离![]() 处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为
处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为![]() 时,达到最大高度
时,达到最大高度![]() ,然后准确落入篮筐内,已知篮圈中心距离地面高度为
,然后准确落入篮筐内,已知篮圈中心距离地面高度为![]() ,试解答下列问题:
,试解答下列问题:
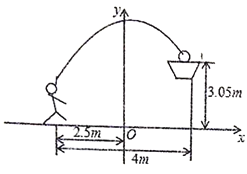
(1)建立图中所示的平面直角坐标系,求抛物线所对应的函数表达式.
(2)这次跳投时,球出手处离地面多高?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如表:
的部分对应值如表:
|
| 0 | 2 | 3 | 4 |
| 5 | 0 |
|
| 0 |
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() ;④3是方程
;④3是方程![]() 的一个根;⑤若
的一个根;⑤若![]() ,
,![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中正确的个数是( )
,其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,对于二次函数![]() ,下列说法:①
,下列说法:①![]() 的最小值为1;②图象顶点坐标为
的最小值为1;②图象顶点坐标为![]() ,对称轴为直线
,对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而增大,当
值的增大而增大,当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而减小;④它的图象可以由
值的增大而减小;④它的图象可以由![]() 的图象向右平移2个单位长度,再向上平移1个单位长度得到。其中错误的个数是( )
的图象向右平移2个单位长度,再向上平移1个单位长度得到。其中错误的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产并进行治污改造,其月利润![]() (万元)与月份
(万元)与月份![]() 之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的部分,下列选项错误的是( )
之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的部分,下列选项错误的是( )
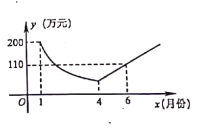
A.4月份的利润为![]() 万元
万元
B.污改造完成后每月利润比前一个月增加![]() 万元
万元
C.治污改造完成前后共有![]() 个月的利润低于
个月的利润低于![]() 万元
万元
D.9月份该厂利润达到![]() 万元
万元
查看答案和解析>>
科目: 来源: 题型:
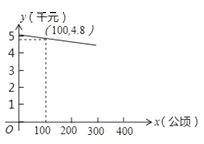
【题目】大豆是一种非常受欢迎的农作物,已知种植某种大豆的平均产量为![]() 吨/公顷,所需成本为8千元/公顷,某地销售大豆的单价
吨/公顷,所需成本为8千元/公顷,某地销售大豆的单价![]() 千元/吨与种植大豆的面积
千元/吨与种植大豆的面积![]() 公顷之间关系如图所示:
公顷之间关系如图所示:
为了鼓励农民种植粮食的热情,市政府出台相关政策:对本市种植大豆的农民按保护价4.5千元/吨进行补偿(即当销售单价低于4.5千元/吨时,差价由政府提供补助,比如销售单价为4千元/吨,则政府补贴农民0.5千元/吨,若单价不少于4.5千元/吨时,则不补助)。
(1)若该市计划种植大豆300公顷,销售后是否享受政府补贴?若享受则享受补贴总金额是多少千元?
(2)设该市销售大豆获得的利润(不含政府补贴部分)为w千元,当种植面积为多少公顷时利润最大,最大利润是多少千元?注:销售利润=(销售单价×每公顷产量-每公顷成本)×公顷数
(3)为保证所得的总利润(含可能得到的政府补贴)达到748千元,应该种植多少公顷大豆?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,P 为△ABC 内一点,连接 PA、PB、PC,在△PAB、△PBC 和△PAC 中,如果存在一个三角形与△ABC 相似,那么就称 P 为△ABC 的自相似点.
(1)如图 2,已知 Rt△ABC 中,∠ACB=90°,CD 是 AB 上的中线,过点 B 作 BE⊥CD,垂足为 E,试说明 E 是△ABC 的自相似点.
(2)如图 3,在△ABC 中,∠A<∠B<∠C.若△ABC 的三个内角平分线的交 点 P 是该 三角形的自相似点,求该三角形三个内角的度数.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在某场足球比赛中,球员甲从球门底部中心点![]() 的正前方
的正前方![]() 处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为
处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为![]() 时达到最高点,此时足球飞行的水平距离为
时达到最高点,此时足球飞行的水平距离为![]() .已知球门的横梁高
.已知球门的横梁高![]() 为
为![]() .
.

![]() 在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
![]() 守门员乙站在距离球门
守门员乙站在距离球门![]() 处,他跳起时手的最大摸高为
处,他跳起时手的最大摸高为![]() ,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com