
科目: 来源: 题型:
【题目】如图所示,菱形ABCD位于平面直角坐标系中,抛物线y=ax2+bx+c经过菱形的三个顶点A、B、C,已知A(﹣3,0)、B(0,﹣4).
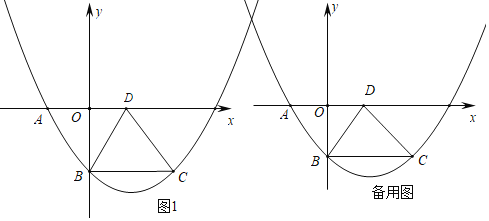
(1)求抛物线解析式;
(2)线段BD上有一动点E,过点E作y轴的平行线,交BC于点F,若S△BOD=4S△EBF,求点E的坐标;
(3)抛物线的对称轴上是否存在点P,使△BPD是以BD为斜边的直角三角形?如果存在,求出点P的坐标;如果不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
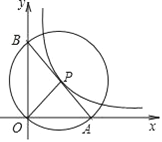
【题目】如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数![]() 图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
(1)求证:P为线段AB的中点;
(2)求△AOB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣8 | ﹣3 | 0 | 1 | 0 | ﹣3 | … |
若A(m,y1),B(m﹣1,y2)两点都在该函数的图象上,当m满足范围_____时,y1<y2.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,点A(3,3),点B(4,0),点C(0,-1).
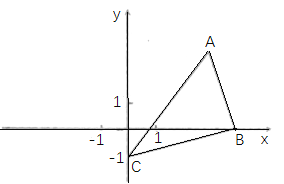
(1)以点C为中心,把△ABC逆时针旋转90°,画出旋转后的图形△A’B’C’(要求尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,
①点A经过的路径AA’的长为________;(结果保留![]() )
)
②写出B’的坐标为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,
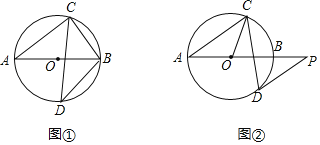
(1)如图①,若D为弧AB的中点,求∠ABC和∠ABD的大小;
(2)如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线G:y=mx2+2mx+m﹣1(m≠0)与y轴交于点C,抛物线G的顶点为D,直线:y=mx+m﹣1(m≠0).

(1)当m=1时,画出直线和抛物线G,并直接写出直线被抛物线G截得的线段长.
(2)随着m取值的变化,判断点C,D是否都在直线上并说明理由.
(3)若直线被抛物线G截得的线段长不小于2,结合函数的图象,直接写出m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】给出如下定义:对于⊙O的弦MN和⊙O外一点P(M,O,N三点不共线,且点P,O在直线MN的异侧),当∠MPN+∠MON=180°时,则称点P是线段MN关于点O的关联点.图1是点P为线段MN关于点O的关联点的示意图.
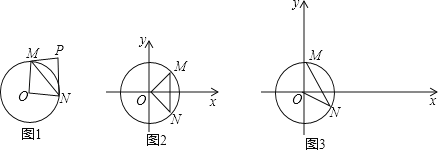
在平面直角坐标系xOy中,⊙O的半径为1.
(1)如图2,已知M(![]() ,
,![]() ),N(
),N(![]() ,﹣
,﹣![]() ),在A(1,0),B(1,1),C(
),在A(1,0),B(1,1),C(![]() ,0)三点中,是线段MN关于点O的关联点的是 ;
,0)三点中,是线段MN关于点O的关联点的是 ;
(2)如图3,M(0,1),N(![]() ,﹣
,﹣![]() ),点D是线段MN关于点O的关联点.
),点D是线段MN关于点O的关联点.
①∠MDN的大小为 ;
②在第一象限内有一点E(![]() m,m),点E是线段MN关于点O的关联点,判断△MNE的形状,并直接写出点E的坐标;
m,m),点E是线段MN关于点O的关联点,判断△MNE的形状,并直接写出点E的坐标;
③点F在直线y=﹣![]() x+2上,当∠MFN≥∠MDN时,求点F的横坐标x的取值范围.
x+2上,当∠MFN≥∠MDN时,求点F的横坐标x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
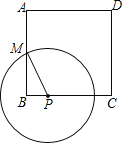
【题目】如图,正方形ABCD的边长为6,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】运动员将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间t(s)满足二次函数关系,t与h的几组对应值如下表所示.
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度;
(3)问:小球的飞行高度能否达到22m?请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的一元二次方程x2+2(m﹣1)x+m2﹣3=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为非负整数,且该方程的根都是无理数,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com