
科目: 来源: 题型:
【题目】如图,已知AB为⊙O的直径,CD切⊙O于C点,弦CF⊥AB于E点,连结AC.

(1)求证:∠ACD=∠ACF;
(2)当AD⊥CD,BE=2cm,CF=8cm,求AD的长.
查看答案和解析>>
科目: 来源: 题型:
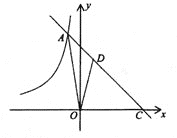
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与函数
的图象与函数![]() 的图象相交于点A,并与
的图象相交于点A,并与![]() 轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
(1)求![]() 的值;
的值;
(2)求点D的坐标;
(3)根据图象,直接写出当![]() 时不等式
时不等式![]() 的
的![]() 的解集.
的解集.
查看答案和解析>>
科目: 来源: 题型:
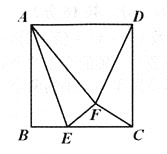
【题目】如图,点E是边长为2的正方形ABCD的边BC上的一动点(不与端点重合),将△ABE沿AE翻折至△AFE的位置,若△CDF是等腰三角形,则BE=________.
查看答案和解析>>
科目: 来源: 题型:
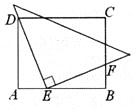
【题目】如图,在矩形ABCD中,AD=6,AB=10,一个三角形的直角顶点E是边AB上的一动点,一直角边过点D,另一直角边与BC交于F,若AE=x,BF=y,则y关于x的函数关系的图象大致为( )
A.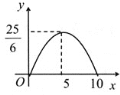 B.
B.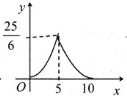 C.
C.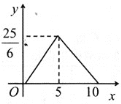 D.
D.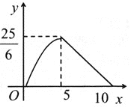
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东55方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
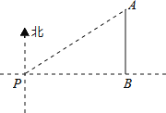
A.2cos55o海里B.![]() 海里C.2sin55海里D.
海里C.2sin55海里D.![]() 海里
海里
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,设D为锐角△ABC内一点,∠ADB=∠ACB+90°,过点B作BE⊥BD,BE=BD,连接EC.
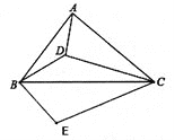
(1)求∠CAD+∠CBD的度数;
(2)若![]() ,
,
①求证:△ACD∽△BCE;
②求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明同学利用寒假30天时间贩卖草莓,了解到某品种草莓成本为10元/千克,在第![]() 天的销售量与销售单价如下(每天内单价和销售量保持一致):
天的销售量与销售单价如下(每天内单价和销售量保持一致):
销售量 |
|
销售单价 | 当 |
当 |
设第![]() 天的利润
天的利润![]() 元.
元.
(1)请计算第几天该品种草莓的销售单价为25元/千克?
(2)这30天中,该同学第几天获得的利润最大?最大利润是多少?注:利润=(售价-成本)×销售量
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB为⊙O的直径,CD切⊙O于C点,弦CF⊥AB于E点,连结AC.
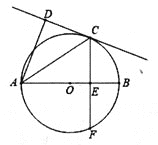
(1)求证:∠ACD=∠ACF;
(2)当AD⊥CD,BE=2cm,CF=8cm,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com