
科目: 来源: 题型:
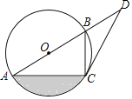
【题目】如图,已知AB是⊙O的直径,C是⊙O上的点,点D在AB的延长线上,∠BCD=∠BAC.
(1)求证:CD是⊙O的切线.
(2)若∠D=30°,BD=2,求⊙O的半径
(3)在(2)的条件下,求图中阴影部分的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)从中任取一张,求取到偶数的概率.
(2)甲、乙两人进行摸牌游戏.
①甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
②若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目: 来源: 题型:
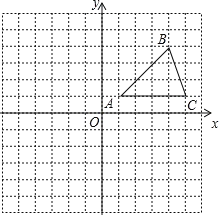
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形)。
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标;
(3)在第(2)问中,点B旋转到点B2的过程中运动的路径长是_____.
查看答案和解析>>
科目: 来源: 题型:
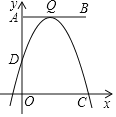
【题目】如图,抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图象如图所示,则下列结论:
之间,其部分图象如图所示,则下列结论:
![]() ;
;
![]() ;
;
![]() 点
点![]() 、
、![]() 、
、![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ;
;
![]() ;
;
![]() (
(![]() 为任意实数).
为任意实数).
其中正确结论的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,线段AB的端点坐标分别为A(0,6)、B(6,6).点Q在线段AB上,以Q为项点的抛物线y=﹣![]() x2+bx+c与y轴交于点D,与x轴的一个交点为C.设点Q的横坐标为m,点C的横坐标为n(n>m).
x2+bx+c与y轴交于点D,与x轴的一个交点为C.设点Q的横坐标为m,点C的横坐标为n(n>m).
(1)当m=0时,求n的值.
(2)求线段AD的长(用含m的式子表示);
(3)点P(2,0)在x轴上,设△BPD的面积为S,求S与m的关系式;
(4)当△DCQ是以QC为直角边的直角三角形时,直接写出m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】(知识回顾)
我们把连结三角形两边中点的线段叫做三角形的中位线,并且有:三角形的中位线平行于第三边,并且等于第三边的一半.
(定理证明)
将下列的定理证明补充完整:
已知:如图①,在△ABC中,点D、E分别是边AB、AC中点,连结DE.
求证:
证明:
(定理应用)
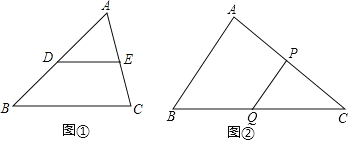
如图②,在△ABC中,AB=10,∠ABC=60°,点P、Q分别是边AC、BC的中点,连结PQ.
(1)线段PQ的长为 .
(2)以点C为一个端点作线段CD(CD与AB不平行),连结AD,取AD的中点M,连结PM、QM.
①在图②中补全图形.
②当∠PQM=∠PMQ时,求CD的长.
③在②的条件下,当△PQM面积最大时,直接写出∠BCD的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图,在矩形ABCD中,AB=8,BC=x(0<x≤8),点E在边CD上,且CE=CB,以AE为对角线作正方形AGEF.设正方形AGEF的面积y.
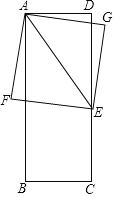
(1)当点F在矩形ABCD的边上时,x= .
(2)求y与x的函数关系式及y的取值范围.
(3)当矩形ABCD的一条边将正方形AGEF的面积分为1:3两部分时,直接写出x的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】利用函数图象探究方程x(|x|﹣2)=![]() 的实数根的个数.
的实数根的个数.
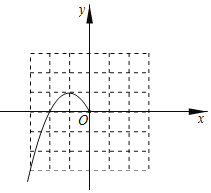
(1)设函数y=x(|x|﹣2),则这个函数的图象与直线y=![]() 的交点的横坐标就是方程x(|x|﹣2)=
的交点的横坐标就是方程x(|x|﹣2)=![]() 的实数根.
的实数根.
(2)分类讨论:当x≤0时,y=﹣x2﹣2x;当x>0时,y= ;
(3)在给定的坐标系中,已经画出了当x≤0时的函数图象,请根据(2)中的解析式,通过描点,连线,画出当x>0时的函数图象.
(4)在给定的坐标系中画直线y=![]() 、观察图象可知方程x(|x|﹣2)=
、观察图象可知方程x(|x|﹣2)=![]() 的实数根有 个.
的实数根有 个.
(5)深入探究:若关于x的方程2x(|x|﹣2)=m有三个不相等的实数根,且这三个实数根的和为负数,则m的取值范围是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,一台灯放置在水平桌面上,底座AB与桌面垂直,底座高AB=5cm,连杆BC=CD=20cm,BC,CD与AB始终在同一平面内.
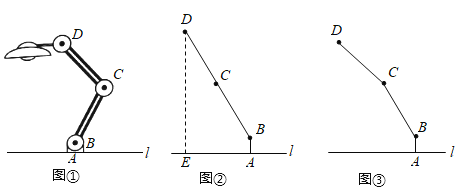
(1)如图②,转动连杆BC,CD,使∠BCD成平角,∠ABC=143°,求连杆端点D离桌面l的高度DE.
(2)将图②中的连杆CD再绕点C逆时针旋转16°,如图③,此时连杆端点D离桌面l的高度减小了 cm.
(参考数据:sin37°=0.6,cos37°=0.8,tan37°=0.75)
查看答案和解析>>
科目: 来源: 题型:
【题目】在硬地上抛掷一枚图钉,通常会出现两种情况:

下面是小明和同学做“抛掷图钉实验”获得的数据:
抛掷次数n | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
针尖不着地的频数m | 63 | 120 | 186 | 252 | 310 | 360 | 434 | 488 | 549 | 610 |
针尖不着地的频率 | 0.63 | 0.60 | 0.63 | 0.60 | 0.62 | 0.61 |
(1)填写表中的空格;
(2)画出该实验中,抛掷图钉钉尖不着地频率的折线统计图;

(3)根据“抛掷图钉实验”的结果,估计“钉尖着地”的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com