
科目: 来源: 题型:
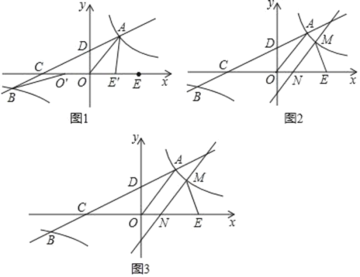
【题目】如图1,在平面直角坐标系xOy中,双曲线![]() 与直线y=ax+b(a≠0)交于A、B两点,直线AB分别交x轴、y轴于C、D两点,E为x轴上一点.已知OA=OC=OE,A点坐标为(3,4).
与直线y=ax+b(a≠0)交于A、B两点,直线AB分别交x轴、y轴于C、D两点,E为x轴上一点.已知OA=OC=OE,A点坐标为(3,4).
(1)将线段OE沿x轴平移得线段O′E′(如图1),在移动过程中,是否存在某个位置使|BO′﹣AE′|的值最大?若存在,求出|BO′﹣AE′|的最大值及此时点O′的坐标;若不存在,请说明理由;
(2)将直线OA沿射线OE平移,平移过程中交![]() 的图象于点M(M不与A重合),交x轴于点N(如图3).在平移过程中,是否存在某个位置使△MNE为以MN为腰的等腰三角形?若存在,求出M的坐标;若不存在,请说明理由.
的图象于点M(M不与A重合),交x轴于点N(如图3).在平移过程中,是否存在某个位置使△MNE为以MN为腰的等腰三角形?若存在,求出M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
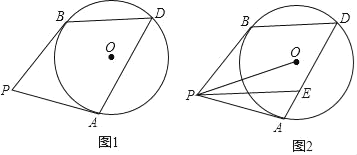
【题目】如图,PA、PB是⊙O的切线,A,B为切点,D为⊙O上一点.
(1)求证:∠P=180°﹣2∠D;
(2)如图,PE∥BD交AD于点E,若DE=2AE,tan∠OPE=![]() ,⊙O的半径为2
,⊙O的半径为2![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学原计划加工一批校服,现有甲、乙两个工厂加工这批校服,已知甲工厂每天能加工这种校服16件,乙工厂每天加工这种校服24件,且单独加工这批校服甲厂比乙厂要多用20天
(1)求这批校服共有多少件?
(2)为了尽快完成这批校服,若先由甲、乙两工厂按原速度合作一段时间后,甲工厂停工,而乙工厂每天的速度提高25%,乙工厂单独完成剩下的部分,且乙工厂全部工作时间是甲工厂工作时间的2倍还多4天,求乙工厂加工多少天
查看答案和解析>>
科目: 来源: 题型:
【题目】定安县定安中学初中部三名学生竞选校学生会主席,他们的笔试成绩和演讲成绩(单位:分)分别用两种方式进行统计,如表和图.
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 |
| 80 | 85 |
(1)请将表和图中的空缺部分补充完整;
(2)图中B同学对应的扇形圆心角为 度;
(3)竞选的最后一个程序是由初中部的300名学生进行投票,三名候选人的得票情况如图(没有弃权票,每名学生只能推荐一人),则A同学得票数为 ,B同学得票数为 ,C同学得票数为 ;
(4)若每票计1分,学校将笔试、演讲、得票三项得分按4:3:3的比例确定个人成绩,请计算三名候选人的最终成绩,并根据成绩判断 当选.(从A、B、C、选择一个填空)

查看答案和解析>>
科目: 来源: 题型:
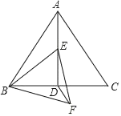
【题目】如图,在边长为2的等边△ABC中,D是BC的中点,点E在线段AD上,连结BE,在BE的下方作等边△BEF,连结DF.当△BDF的周长最小时,∠DBF的度数是_____.
查看答案和解析>>
科目: 来源: 题型:
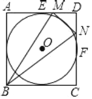
【题目】如图,⊙O内切于正方形ABCD,边AD、CD分别与⊙O切于点E、F,点M、N分别在线段DE、DF上,且MN与⊙O相切,若△MBN的面积为8,则⊙O的半径为( )
A.![]() B.2
B.2![]() C.
C.![]() D.2
D.2![]()
查看答案和解析>>
科目: 来源: 题型:
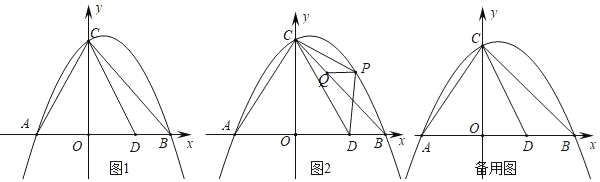
【题目】如图1,抛物线与y=﹣![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC,点D是线段AB上一点,且AD=CA,连接CD.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC,点D是线段AB上一点,且AD=CA,连接CD.
(1)如图2,点P是直线BC上方抛物线上的一动点,在线段BC上有一动点Q,连接PC、PD、PQ,当△PCD面积最大时,求PQ+![]() CQ的最小值;
CQ的最小值;
(2)将过点D的直线绕点D旋转,设旋转中的直线l分别与直线AC、直线CO交于点M、N,当△CMN为等腰三角形时,直接写出CM的长.
查看答案和解析>>
科目: 来源: 题型:
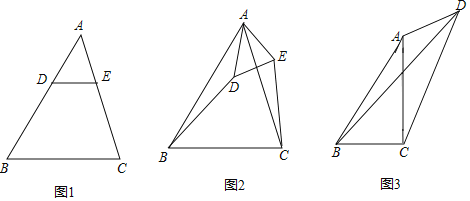
【题目】(1)如图1,在△ABC中,AB>AC,点D,E分别在边AB,AC上,且DE∥BC,若AD=2,AE=![]() ,则
,则![]() 的值是 ;
的值是 ;
(2)如图2,在(1)的条件下,将△ADE绕点A逆时针方向旋转一定的角度,连接CE和BD,![]() 的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;
的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;
(3)如图3,在四边形ABCD中,AC⊥BC于点C,∠BAC=∠ADC=θ,且tanθ=![]() ,当CD=6,AD=3时,请直接写出线段BD的长度.
,当CD=6,AD=3时,请直接写出线段BD的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,BD是平行四边形ABCD的对角线,DE⊥AB于点E,过点E的直线交BC于点G,且BG=CG.
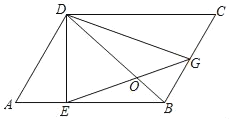
(1)求证:GD=EG.
(2)若BD⊥EG垂足为O,BO=2,DO=4,画出图形并求出四边形ABCD的面积.
(3)在(2)的条件下,以O为旋转中心顺时针旋转△GDO,得到△G′D'O,点G′落在BC上时,请直接写出G′E的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com