科目： 来源： 题型：
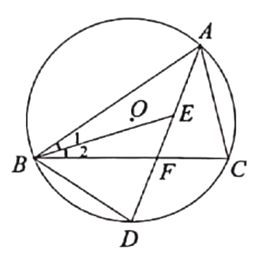
【题目】如图，△ABC内接于⊙O，∠ABC和 ∠BAC的平分线交于点E，延长AE分别交BC， ⊙O于点F， D，连接BD.
(1)求证: BD=DE.
(2)若BD=6，AD=10，求EF的长.
查看答案和解析>>
科目： 来源： 题型：
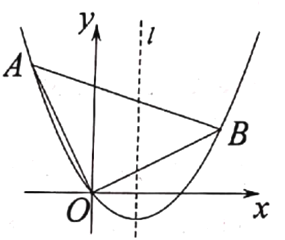
【题目】在平面直角坐标系中，△AOB的位置如图所示，∠AOB=90°，AO=BO，点A的坐标为(-1， 2) .抛物线y = ax2 + bx (a≠0)恰好经过A， B两点.
(1)直接写出点B坐标 .
(2)求该抛物线的函数表达式.
(3)设A关于抛物线的对称轴l的对称点为A'，求△AA' B的面积.
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，在△ABC中，AC=BC=5， AB=6， 点D为AC上一点，作DE//AB交BC于点E，点C关于DE的对称点为点O，以OA为半径作⊙O恰好经过点C，并交直线DE于点M，N.则MN的值为__________.
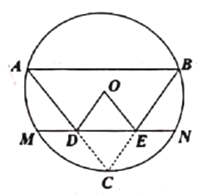
查看答案和解析>>
科目： 来源： 题型：
【题目】我们知道，勾股定理反映了直角三角形三条边的关系: a2+b2=c2， 而a2， b2， c2又可以看成是以a，b， c为边长的正方形的面积.如图，在Rt△ABC中，∠ACB=90°，BC=a， AC=b，O为AB的中点.分别以AC，BC 为边向△ABC外作正方形ACFG，BCED，连结OF， EF， OE，则△OEF的面积为( )
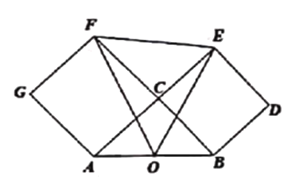
A.
B.
C.
D.
查看答案和解析>>
科目： 来源： 题型：
【题目】某公司需招聘一名员工，对应聘者甲、乙、丙、丁从笔试、面试两个方面进行量化考核.甲、乙、丙、丁两项得分如下表：（单位：分）
甲 | 乙 | 丙 | 丁 | |
笔试 |
|
|
|
|
面试 |
|
|
|
|
（1）这
名选手笔试成绩的中位数是____________分，面试的众数是_____________分；
（2）该公司规定：笔试、面试分别按
，
的比例计总分，请比较甲、乙的总分的大小.
查看答案和解析>>
科目： 来源： 题型：
【题目】超越公司将某品牌农副产品运往新时代市场进行销售，记汽车行驶时为t小时，平均速度为v千米/小时（汽车行驶速度不超过100千米/小时）．根据经验，v，t的一组对应值如下表：
v（千米/小时） | 75 | 80 | 85 | 90 | 95 |
t（小时） | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
（1）根据表中的数据，求出平均速度v（千米/小时）关于行驶时间t（小时）的函数表达式；
（2）汽车上午7：30从超越公司出发，能否在上午10：00之前到达新时代市场？请说明理由．
查看答案和解析>>
科目： 来源： 题型：
【题目】“早黑宝”葡萄品种是我省农科院研制的优质新品种，在我省被广泛种植，邓州市某葡萄种植基地2017年种植“早黑宝”100亩，到2019年“卓黑宝”的种植面积达到196亩.
（1）求该基地这两年“早黑宝”种植面积的平均增长率；
（2）市场调查发现，当“早黑宝”的售价为20元/千克时，每天能售出200千克，售价每降价1元，每天可多售出50千克，为了推广宣传，基地决定降价促销，同时减少库存，已知该基地“早黑宝”的平均成本价为12元/千克，若使销售“早黑宝”每天获利1750元，则售价应降低多少元？
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，半圆D的直径AB＝4，线段OA＝7，O为原点，点B在数轴的正半轴上运动，点B在数轴上所表示的数为m．
（1）当半圆D与数轴相切时，m＝ ．
（2）半圆D与数轴有两个公共点，设另一个公共点是C．
①直接写出m的取值范围是 ．
②当BC＝2时，求△AOB与半圆D的公共部分的面积．
（3）当△AOB的内心、外心与某一个顶点在同一条直线上时，求tan∠AOB的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
