
科目: 来源: 题型:
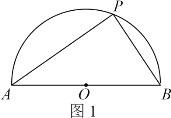
【题目】(问题发现)如图1,半圆O的直径AB=10,点P是半圆O上的一个动点,则△PAB的面积最大值是 ;
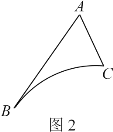
(问题探究)如图2所示,AB、AC、![]() 是某新区的三条规划路,其中AB=6km,AC=3km,∠BAC=60°,
是某新区的三条规划路,其中AB=6km,AC=3km,∠BAC=60°,![]() 所对的圆心角为60°.新区管委会想在
所对的圆心角为60°.新区管委会想在![]() 路边建物资总站点P,在AB、AC路边分别建物资分站点E、F,即分别在
路边建物资总站点P,在AB、AC路边分别建物资分站点E、F,即分别在![]() 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.显然,为了快捷环保和节约成本,就要使线段PE、EF、FP之和最短(各物资站点与所在道路之间的距离、路宽均忽略不计).可求得△PEF周长的最小值为 km;
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.显然,为了快捷环保和节约成本,就要使线段PE、EF、FP之和最短(各物资站点与所在道路之间的距离、路宽均忽略不计).可求得△PEF周长的最小值为 km;
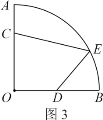
(拓展应用)如图3是某街心花园的一角,在扇形OAB中,∠AOB=90°,OA=12米,在围墙OA和OB上分别有两个入口C和D,且AC=4米,D是OB的中点,出口E在![]() 上.现准备沿CE、DE从入口到出口铺设两条景观小路,在四边形CODE内种花,在剩余区域种草.
上.现准备沿CE、DE从入口到出口铺设两条景观小路,在四边形CODE内种花,在剩余区域种草.
①出口E设在距直线OB多远处可以使四边形CODE的面积最大?最大面积是多少?(小路宽度不计)
②已知铺设小路CE所用的普通石材每米的造价是200元,铺设小路DE所用的景观石材每米的造价是400元.
请问:在![]() 上是否存在点E,使铺设小路CE和DE的总造价最低?若存在,求出最低总造价和出口E距直线OB的距离;若不存在,请说明理由.
上是否存在点E,使铺设小路CE和DE的总造价最低?若存在,求出最低总造价和出口E距直线OB的距离;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,二次函数 y=ax2+bx+2 的图象与 x 轴交于 A(﹣3,0),B(1,0)两点,与 y 轴交于点C.
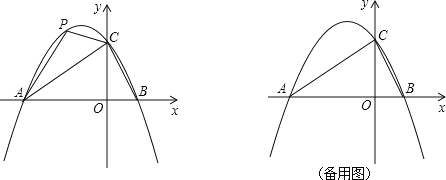
(1)求这个二次函数的关系解析式 ,x 满足什么值时 y﹤0 ?
(2)点 p 是直线 AC 上方的抛物线上一动点,是否存在点 P,使△ACP 面积最大?若存在,求出点 P的坐标;若不存在,说明理由
(3)点 M 为抛物线上一动点,在 x 轴上是否存在点 Q,使以 A、C、M、Q 为顶点的四边形是平行四边形?若存在,直接写出点 Q 的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司研制出新产品,该产品的成本为每件2400元.在试销期间,购买不超过10件时,每件销售价为3000元;购买超过10件时,每多购买一件,所购产品的销售单价均降低5元,但最低销售单价为2600元。请解决下列问题:
(1)直接写出:购买这种产品 ________件时,销售单价恰好为2600元;
(2)设购买这种产品x件(其中x>10,且x为整数),该公司所获利润为y元,求y与x之间的函数表达式;
(3)该公司的销售人员发现:当购买产品的件数超过10件时,会出现随着数量的增多,公司所获利润反而减少这一情况.为使购买数量越多,公司所获利润越大,公司应将最低销售单价调整为多少元?(其它销售条件不变)
查看答案和解析>>
科目: 来源: 题型:
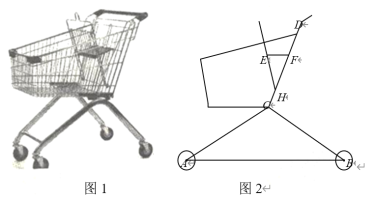
【题目】如图1是超市的手推车,如图2是其侧面示意图,已知前后车轮半径均为5 cm,两个车轮的圆心的连线AB与地面平行,测得支架AC=BC=60cm,AC、CD所在直线与地面的夹角分别为30°、60°,CD=50cm.
(1)求扶手前端D到地面的距离;
(2)手推车内装有简易宝宝椅,EF为小坐板,打开后,椅子的支点H到点C的距离为10 cm,DF=20cm,EF∥AB,∠EHD=45°,求坐板EF的宽度.(本题答案均保留根号)
查看答案和解析>>
科目: 来源: 题型:
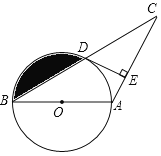
【题目】已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线.
(2)若⊙O的半径为3cm,∠C=30°,求图中阴影部分的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 三个顶点的坐标分别
三个顶点的坐标分别![]() .
.
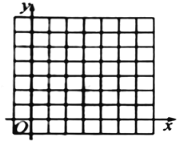
(1)画出![]() ;
;
(2)以B为位似中心,将![]() 放大到原来的2倍,在右图的网格图中画出放大后的图形△
放大到原来的2倍,在右图的网格图中画出放大后的图形△![]() ;
;
(3)写出点A的对应点![]() 的坐标:___.
的坐标:___.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校九年级学生某科目学期总评成绩是由完成作业、单元检测、期末考试三项成绩构成的,如果学期总评成绩80分以上(含80分),则评定为“优秀”,下表是小张和小王两位同学的成绩记录:
完成作业 | 单元测试 | 期末考试 | |
小张 | 70 | 90 | 80 |
小王 | 60 | 75 | _______ |
若按完成作业、单元检测、期末考试三项成绩按1:2:7的权重来确定学期总评成绩.
(1)请计算小张的学期总评成绩为多少分?
(2)小王在期末(期末成绩为整数)应该最少考多少分才能达到优秀?
查看答案和解析>>
科目: 来源: 题型:
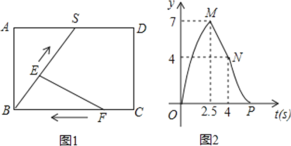
【题目】如图1,S是矩形ABCD的AD边上一点,点E以每秒kcm的速度沿折线BS-SD-DC匀速运动,同时点F从点C出发点,以每秒1cm的速度沿边CB匀速运动.已知点F运动到点B时,点E也恰好运动到点C,此时动点E,F同时停止运动.设点E,F出发t秒时,△EBF的面积为![]() .已知y与t的函数图像如图2所示.其中曲线OM,NP为两段抛物线,MN为线段.则下列说法:
.已知y与t的函数图像如图2所示.其中曲线OM,NP为两段抛物线,MN为线段.则下列说法:
①点E运动到点S时,用了2.5秒,运动到点D时共用了4秒;
②矩形ABCD的两邻边长为BC=6cm,CD=4cm;
③sin∠ABS=![]() ;
;
④点E的运动速度为每秒2cm.其中正确的是( )
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知顶点为C(0,﹣3)的抛物线D1:y=ax2+b(a≠0)与x轴交于A,B两点,直线L:y=x+m过顶点C和点B.
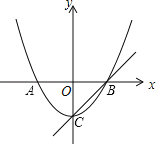
(1)求抛物线D1:y=ax2+b(a≠0)的解析式;
(2)点D(0,![]() ),在x轴上任取一点Q(x,0),连接DQ,作线段DQ的垂直平分线l1,过点Q作x轴的垂线,记l2,l2与l1的交点为P(x,y),在x轴上多次改变点Q的位置,相应的点P也在坐标系中形成了曲线路径D2,写出点P(x,y)的路径D2所满足的关系式(即x,y所满足的关系式),能否通过平移、轴对称或旋转变换,由抛物线D1得到曲线D2?请说明理由.
),在x轴上任取一点Q(x,0),连接DQ,作线段DQ的垂直平分线l1,过点Q作x轴的垂线,记l2,l2与l1的交点为P(x,y),在x轴上多次改变点Q的位置,相应的点P也在坐标系中形成了曲线路径D2,写出点P(x,y)的路径D2所满足的关系式(即x,y所满足的关系式),能否通过平移、轴对称或旋转变换,由抛物线D1得到曲线D2?请说明理由.
(3)抛物线D1上是否存在点M,使得∠MCB=15°?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,△ABC,△CDE都是等边三角形.
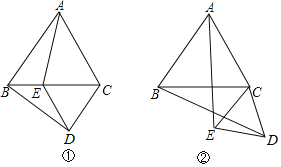
(1)写出AE与BD的大小关系.
(2)若把△CDE绕点C逆时针旋转到图②的位置时,上述(1)的结论仍成立吗?请说明理由.
(3)△ABC的边长为5,△CDE的边长为2,把△CDE绕点C逆时针旋转一周后回到图①位置,求出线段AE长的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com