
科目: 来源: 题型:
【题目】若整数a使关于x的分式方程![]() =2有整数解,且使关于x的不等式组
=2有整数解,且使关于x的不等式组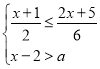 至少有4个整数解,则满足条件的所有整数a的和是( )
至少有4个整数解,则满足条件的所有整数a的和是( )
A.﹣14B.﹣17C.﹣20D.﹣23
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,反比例函数y=![]() (x>0)的图象经过Rt△BOC斜边上的中点A,与边BC交于点D,连接AD,则△ADB的面积为( )
(x>0)的图象经过Rt△BOC斜边上的中点A,与边BC交于点D,连接AD,则△ADB的面积为( )
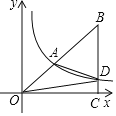
A.12B.16C.20D.24
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与实践
问题情境
在一节数学活动课上,老师带领同学们借助几何画板对以下题目进行了研究.如图1,
MN是过点A的直线,点C为直线MN外一点,连接AC,作∠ACD=60°,使AC=DC,在MN上取一点B,使∠DBN=60°.
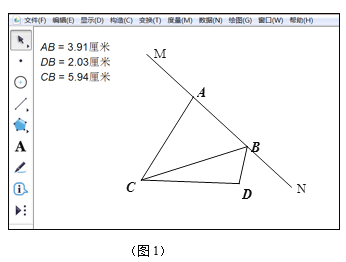
观察发现
(1)根据图1中的数据,猜想线段AB、DB、CB之间满足的数量关系是 ;
(2)希望小组认真思考后提出一种证明方法:将CB所在的直线以点C为旋转中心,逆时针旋转60°,与直线MN交于点E,即可证明(1)中的结论. 请你在图1中作出线段CE,并根据此方法写出证明过程;
实践探究
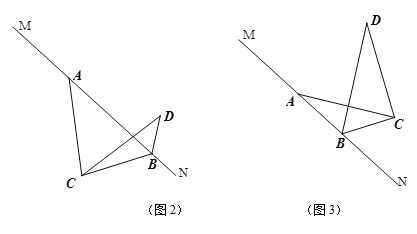
(3)奋进小组在继续探究的过程中,将点C绕点A逆时针旋转,他们发现当旋转到图2和图3的位置时,∠DBN=120°,线段AB、BD、CB的大小发生了变化,但是仍然满足一定的数量关系,请你直接写出这两种关系:
在图2中,线段AB、DB、CB之间满足的数量关系是 ;
在图3中,线段AB、DB、CB之间满足的数量关系是 ;
提出问题
(4)智慧小组提出一个问题:若图3中BC⊥CD于点C时,BC=2,则AC为多长?请你解答此问题.
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与探究
如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B两点,与y轴交于点C,对称轴为x=1.
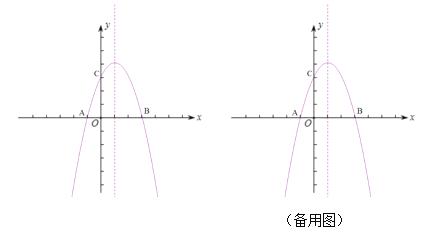
(1)求抛物线的函数表达式;
(2)在抛物线的对称轴上求一点P,使点P到点A的距离与到点C的距离之和最小,并求出此时点P的坐标;
(3)是否存在过A,B两点的抛物线,其顶点M关于x轴的对称点为N,使得四边形AMBN为正方形?若存在,请直接写出此抛物线的函数表达式;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】小林在使用笔记本电脑时,为了散热,他将电脑放在散热架CAD上,忽略散热架和电脑的厚度,侧面示意图如图1所示,已知电脑显示屏OB与底板OA的夹角为135°,OB=OA=25cm,OE⊥AD于点E,OE=12.5cm.

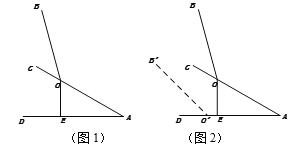
(1)求∠OAE的度数;
(2)若保持显示屏OB与底板OA的135°夹角不变,将电脑平放在桌面上如图2中的![]() 所示,则显示屏顶部
所示,则显示屏顶部![]() 比原来顶部B大约下降了多少?(参考数据:结果精确到0.1cm.参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,
比原来顶部B大约下降了多少?(参考数据:结果精确到0.1cm.参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】请阅读以下材料,并完成相应的任务:

任务:
(1)设P(a,![]() ),R(b,
),R(b,![]() ),求直线OM的函数解析式(用含a,b的代数式表示),并说明Q点在直线OM上;
),求直线OM的函数解析式(用含a,b的代数式表示),并说明Q点在直线OM上;
(2)证明:∠MOB=![]() ∠AOB.
∠AOB.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了了解今年九年级学生的数学学习情况,在中考考前适应性训练测试后,对九年级全体同学的数学成绩作了统计分析,按照成绩高低分为A、B、C、D四个等级并绘制了如图1和图2的统计图(均不完整),请结合图中所给出的信息解答问题:
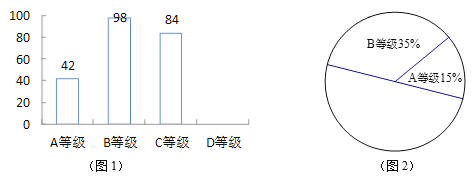
(1)该校九年级学生共有 人.
(2)补全条形统计图与扇形统计图.(要求:请将扇形统计图的空白部分按比例分成两部分.)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O 上一点,过点C作⊙O的切线DE,AD⊥DE于点D,DE与AB的延长线交于点E,连接AC.

(1)求证:AC平分∠DAE;
(2)若⊙O的半径为2,∠CAB=35°,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在数学课上,老师提出如下问题:
如图,已知线段AB,BC,∠ABC = 90°. 求作:矩形ABCD.

小明的作图过程如下:
(1)连接AC,作线段AC的垂直平分线,交AC于M;
(2)连接BM并延长,在延长线上取一点D,使MD=MB,连接AD,CD.
∴四边形ABCD即为所求.

老师说:“小明的作法正确.”
请回答:小明这样作图的依据是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com