
科目: 来源: 题型:
【题目】学校打算用长![]() 米的篱笆围城一个长方形的生物园饲养小兔,生物园的一面靠在长为
米的篱笆围城一个长方形的生物园饲养小兔,生物园的一面靠在长为![]() 米的墙上(如图).
米的墙上(如图).

(1)若生物园的面积为![]() 平方米,求生物园的长和宽;
平方米,求生物园的长和宽;
(2)能否围城面积为![]() 平方米的生物园?若能,求出长和宽;若不能,请说明理由.
平方米的生物园?若能,求出长和宽;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
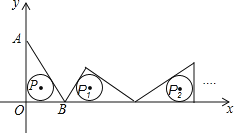
【题目】如图,把![]() 置于平面直角坐标系中,点A的坐标为
置于平面直角坐标系中,点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,点P是
,点P是![]() 内切圆的圆心.将
内切圆的圆心.将![]() 沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合,第一次滚动后圆心为
沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合,第一次滚动后圆心为![]() ,第二次滚动后圆心为
,第二次滚动后圆心为![]() ,…,依此规律,第2019次滚动后,
,…,依此规律,第2019次滚动后,![]() 内切圆的圆心
内切圆的圆心![]() 的坐标是________.
的坐标是________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC是边长为2的等边三角形,点D与点B分别位于直线AC的两侧,且AD=AC, 联结BD、CD,BD交直线AC于点E.
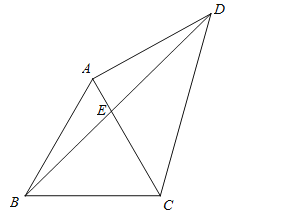

(1)当∠CAD=90°时,求线段AE的长.
(2)过点A作AH⊥CD,垂足为点H,直线AH交BD于点F,
①当∠CAD<120°时,设![]() ,
,![]() (其中
(其中![]() 表示△BCE的面积,
表示△BCE的面积,![]() 表示△AEF的面积),求y关于x的函数关系式,并写出x的取值范围;
表示△AEF的面积),求y关于x的函数关系式,并写出x的取值范围;
②当![]() 时,请直接写出线段AE的长.
时,请直接写出线段AE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,平移一条抛物线,如果平移后的新抛物线经过原抛物线顶点,且新抛物线的对称轴是y轴,那么新抛物线称为原抛物线的“影子抛物线”.
中,平移一条抛物线,如果平移后的新抛物线经过原抛物线顶点,且新抛物线的对称轴是y轴,那么新抛物线称为原抛物线的“影子抛物线”.
(1)已知原抛物线表达式是![]() ,求它的“影子抛物线”的表达式;
,求它的“影子抛物线”的表达式;
(2)已知原抛物线经过点(1,0),且它的“影子抛物线”的表达式是![]() ,求原抛物线的表达式;
,求原抛物线的表达式;
(3)小明研究后提出:“如果两条不重合的抛物线交y轴于同一点,且它们有相同的“影子抛物线”,那么这两条抛物线的顶点一定关于y轴对称.”你认为这个结论成立吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线![]() ,其顶点为A.
,其顶点为A.
(1)写出这条抛物线的开口方向、顶点A的坐标,并说明它的变化情况;
(2)直线BC平行于x轴,交这条抛物线于B、C两点(点B在点C左侧),且![]() ,求点B坐标.
,求点B坐标.
查看答案和解析>>
科目: 来源: 题型:
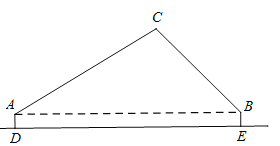
【题目】某数学小组在郊外的水平空地上对无人机进行测高实验.如图,两台测角仪分别放在A、B位置,且离地面高均为1米(即![]() 米),两台测角仪相距50米(即AB=50米).在某一时刻无人机位于点C (点C与点A、B在同一平面内),A处测得其仰角为
米),两台测角仪相距50米(即AB=50米).在某一时刻无人机位于点C (点C与点A、B在同一平面内),A处测得其仰角为![]() ,B处测得其仰角为
,B处测得其仰角为![]() .(参考数据:
.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
(1)求该时刻无人机的离地高度;(单位:米,结果保留整数)
(2)无人机沿水平方向向左飞行2秒后到达点F(点F与点A、B、C在同一平面内),此时于A处测得无人机的仰角为![]() ,求无人机水平飞行的平均速度.(单位:米/秒,结果保留整数)
,求无人机水平飞行的平均速度.(单位:米/秒,结果保留整数)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .直线
.直线![]() .
.
![]() 抛物线的解析式为 .直线
抛物线的解析式为 .直线![]() 的解析式为 ;
的解析式为 ;
![]() 若直线
若直线![]() 与抛物线只有一个公共点,求直线
与抛物线只有一个公共点,求直线![]() 的解析式;
的解析式;
![]() 设抛物线的顶点关于
设抛物线的顶点关于![]() 轴的对称点为
轴的对称点为![]() ,点
,点![]() 是抛物线对称轴上一动点,如果直线
是抛物线对称轴上一动点,如果直线![]() 与抛物线在
与抛物线在![]() 轴上方的部分形成了封闭图形(记为图形
轴上方的部分形成了封闭图形(记为图形![]() ).请结合函数的图象,直接写出点
).请结合函数的图象,直接写出点![]() 的纵坐标
的纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
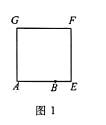
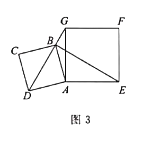
【题目】如图1.正方形![]() 的边长为
的边长为![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
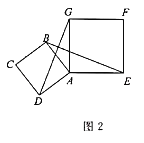
![]() 如图2.将线段
如图2.将线段![]() 绕点
绕点![]() 逆时针旋转,设旋转角为
逆时针旋转,设旋转角为![]() ,并以
,并以![]() 为边作正方形
为边作正方形![]() ,连接
,连接![]() 试问随着线段
试问随着线段![]() 的旋转,
的旋转,![]() 与
与![]() 有怎样的数量关系?说明理由;
有怎样的数量关系?说明理由;
![]() 如图3,在
如图3,在![]() 的条件下,若点
的条件下,若点![]() 恰好落在线段
恰好落在线段![]() 上,求点
上,求点![]() 走过的路径长(保留
走过的路径长(保留![]() ).
).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 且与反比例函数
且与反比例函数![]() 在第一象限的图象交于点
在第一象限的图象交于点![]() 轴于点
轴于点![]() .
.
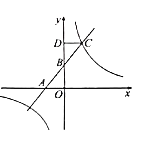
![]() 根据函数图象,直接写出当反比例函数
根据函数图象,直接写出当反比例函数![]() 的函数值
的函数值![]() 时,自变量
时,自变量![]() 的取值范围;
的取值范围;
![]() 动点
动点![]() 在
在![]() 轴上,
轴上,![]() 轴交反比例函数
轴交反比例函数![]() 的图象于点
的图象于点![]() .若
.若![]() .求点
.求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com