
科目: 来源: 题型:
【题目】小明对![]() ,
,![]() ,
,![]() ,
,![]() 四个中小型超市的女工人数进行了统计,并绘制了下面的统计图表,已知
四个中小型超市的女工人数进行了统计,并绘制了下面的统计图表,已知![]() 超市有女工20人.所有超市女工占比统计表
超市有女工20人.所有超市女工占比统计表
超市 |
|
|
|
|
女工人数占比 | 62.5% | 62.5% | 50% | 75% |
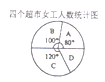
(1)![]() 超市共有员工多少人?
超市共有员工多少人?![]() 超市有女工多少人?
超市有女工多少人?
(2)若从这些女工中随机选出一个,求正好是![]() 超市的概率;
超市的概率;
(3)现在![]() 超市又招进男、女员工各1人,
超市又招进男、女员工各1人,![]() 超市女工占比还是75%吗?甲同学认为是,乙同学认为不是.你认为谁说的对,并说明理由.
超市女工占比还是75%吗?甲同学认为是,乙同学认为不是.你认为谁说的对,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边的高,点
边的高,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,点
轴上,点![]() 在第一象限,若
在第一象限,若![]() 从原点出发,沿
从原点出发,沿![]() 轴向右以每秒1个单位长的速度运动,则点
轴向右以每秒1个单位长的速度运动,则点![]() 随之沿
随之沿![]() 轴下滑,并带动
轴下滑,并带动![]() 在平面内滑动,设运动时间为
在平面内滑动,设运动时间为![]() 秒,当
秒,当![]() 到达原点时停止运动
到达原点时停止运动
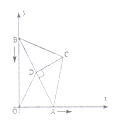
(1)连接![]() ,线段
,线段![]() 的长随
的长随![]() 的变化而变化,当
的变化而变化,当![]() 最大时,
最大时,![]() ______.
______.
(2)当![]() 的边与坐标轴平行时,
的边与坐标轴平行时,![]() ______.
______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
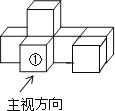
A. 主视图不变,左视图不变
B. 左视图改变,俯视图改变
C. 主视图改变,俯视图改变
D. 俯视图不变,左视图改变
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数y=x2+bx–1的图象如图,对称轴为直线x=1,若关于x的一元二次方程x2–2x–1–t=0(t为实数)在–1<x<4的范围内有实数解,则t的取值范围是

A. t≥–2 B. –2≤t<7
C. –2≤t<2 D. 2<t<7
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某射击运动员练习射击,5次成绩分别是:8、9、7、8、x(单位:环).下列说法中正确的是( )
A. 若这5次成绩的中位数为8,则x=8
B. 若这5次成绩的众数是8,则x=8
C. 若这5次成绩的方差为8,则x=8
D. 若这5次成绩的平均成绩是8,则x=8
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,点O(0,0),点A(1,0).已知抛物线y=x2+mx﹣2m(m是常数),顶点为P.
(Ⅰ)当抛物线经过点A时,求顶点P的坐标;
(Ⅱ)若点P在x轴下方,当∠AOP=45°时,若函数值y>0,求对应自变量x的取值范围;
(Ⅲ)无论m取何值,该抛物线都经过定点H.当∠AHP=45°时,求抛物线的解析式.
查看答案和解析>>
科目: 来源: 题型:
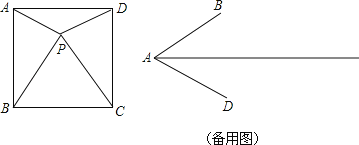
【题目】定义:点P是四边形ABCD内一点,若三角形△PAB,△PBC,△PCD,△PDA均为等腰三角形,则称点P是四边形ABCD的一个“准中心”,如,正方形的中心就是它的一个“准中心”.
(1)如图,已知点P是正方形ABCD内的一点,且∠PBC=∠PCB=60°,证明点P是正四边形ABCD的一个“准中心”;
(2)填空:正方形ABCD共有 个“准中心”;
(3)已知∠BAD=60°,AB=AD=6,点C是∠BAD平分线上的动点,问在四边形ABCD的对角线AC上最多存在几个“准中心”点P(自行画出示意图),并求出每个“准中心”点P对应线段AC的长(精确到个位).
查看答案和解析>>
科目: 来源: 题型:
【题目】知识背景:
当a>0且x>0时,因为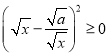 ,所以x﹣2
,所以x﹣2![]() ≥0,从而
≥0,从而![]() (当
(当![]() ,即x=
,即x=![]() 时取等号).
时取等号).
设函数y=x+![]() (x>0,a>0),由上述结论可知:当x=
(x>0,a>0),由上述结论可知:当x=![]() 时,该函数有最小值2
时,该函数有最小值2![]() .
.
应用举例
已知函数为y1=x(x>0)与函数y2=![]() (x>0),则当x=
(x>0),则当x=![]() 时,y1+y2=x+
时,y1+y2=x+![]() 有最小值为2
有最小值为2![]() .
.
解决问题
(1)已知函数为y1=x﹣1(x>1)与函数y2=(x﹣1)2+9(x>1),当x取何值时,![]() 有最小值?最小值是多少?
有最小值?最小值是多少?
(2)已知某设备租赁使用成本包含以下三部分:一是设备的安装调试费用,共490元;二是设备的租赁使用费用,每天200元;三是设备的折旧费用,它与使用天数的平方成正比,比例系数为0.001.若设该设备的租赁使用天数为x天,则当x取何值时,该设备平均每天的租赁使用成本最低?最低是多少元?
查看答案和解析>>
科目: 来源: 题型:
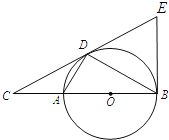
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,若BC=4,tan∠ABD=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com