
科目: 来源: 题型:
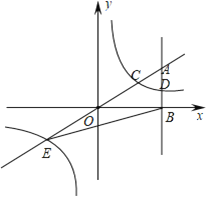
【题目】如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,![]() =
=![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为
的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为![]() .
.
(1)求反比例函数的解析式及点E的坐标;
(2)连接BC,求S△CEB.
(3)若在x轴上的有两点M(m,0)N(-m,0).
①以E、M、C、N为顶点的四边形能否为矩形?如果能求出m的值,如果不能说明理由.
②若将直线OA绕O点旋转,仍与y=![]() 交于C、E,能否构成以E、M、C、N为顶点的四边形为菱形,如果能求出m的值,如果不能说明理由.
交于C、E,能否构成以E、M、C、N为顶点的四边形为菱形,如果能求出m的值,如果不能说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与实践
在数学活动课上,老师给出如下问题,让同学们展开探究活动:
[问题情境]
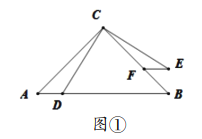
如图①,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 上一点
上一点![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到的对应线段为
,得到的对应线段为![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,请你根据上述条件,提出恰当的数学问题并解答.
,请你根据上述条件,提出恰当的数学问题并解答.
[解决问题]
下面是学习小组提出的三个问题,请你解答这些问题:
(1)“兴趣”组提出的问题是:求证:![]() ;
;
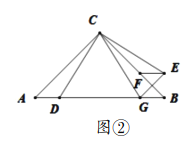
(2)“实践”小组提出的问题是:如图②,若将![]() 沿
沿![]() 的垂直平分线对折,得到
的垂直平分线对折,得到![]() ,连接
,连接![]() ,则线段
,则线段![]() 与
与![]() 有怎样的数量关系?请说明理由;
有怎样的数量关系?请说明理由;
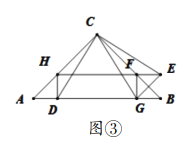
(3)“奋进”小组在“实践”小组探究的基础上,提出了如下问题:延长![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,求证:四边形
,求证:四边形![]() 是矩形.
是矩形.
查看答案和解析>>
科目: 来源: 题型:
【题目】关公,作为运城乃至山西的一张名片,吸引了来自世界各地的游客,在运城西南![]() 公里的常平村(关公故乡)南山上,有一尊巨型关公铜像,高
公里的常平村(关公故乡)南山上,有一尊巨型关公铜像,高![]() 米,象征关公享年
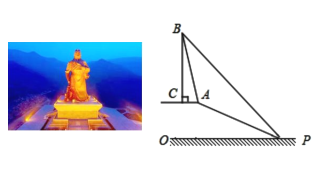
米,象征关公享年![]() 岁,底座的高度也有一定寓意.有一位游客,对此产生了兴趣,想测量它的高度,由于游客无法直接到达铜像底部,因此该游客计划借助坡面高度来测量它的高度.如图,
岁,底座的高度也有一定寓意.有一位游客,对此产生了兴趣,想测量它的高度,由于游客无法直接到达铜像底部,因此该游客计划借助坡面高度来测量它的高度.如图,![]() 代表底座的高,坡顶
代表底座的高,坡顶![]() 与底座底部
与底座底部![]() 处在同一水平面上,该游客在斜坡底
处在同一水平面上,该游客在斜坡底![]() 处测得该底座顶端
处测得该底座顶端![]() 的仰角为
的仰角为![]() ,然后他沿着坡度为
,然后他沿着坡度为![]() 的斜坡
的斜坡![]() 攀行了
攀行了![]() 米,在坡顶
米,在坡顶![]() 处又测得该底座顶端
处又测得该底座顶端![]() 的仰角为
的仰角为![]() .求:
.求:
![]() 坡顶
坡顶![]() 到地面
到地面![]() 的距离;
的距离;
![]() 求底座
求底座![]() 的高度(结果精确到
的高度(结果精确到![]() 米).
米).
(参考数据:![]() ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在大家的期盼中,我区某农贸市场于2009年12月9日盛大开业,王阿姨以每斤![]() 元的价格购进山药若干斤,然后以每斤
元的价格购进山药若干斤,然后以每斤![]() 元的价格出售,每天可售出
元的价格出售,每天可售出![]() 斤.通过调查发现,这种山药每斤的售价每降低
斤.通过调查发现,这种山药每斤的售价每降低![]() 元,每天可多售出
元,每天可多售出![]() 斤.为了保证每天至少售出
斤.为了保证每天至少售出![]() 斤,王阿姨决定降价销售.
斤,王阿姨决定降价销售.
(1)若将这种山药每斤的售价降低![]() 元,则每天的销售量是______斤(用含
元,则每天的销售量是______斤(用含![]() 的代数式表示);
的代数式表示);
(2)销售这种山药要想每天盈利![]() 元,王阿姨需将每斤的售价降低多少元?
元,王阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元二次方程,把它转化为两个一元一次方程来解,求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验,各类方程的解法不尽相同,但是它们有一个共同的基本数学思想“转化”,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.
例如:解方程![]()
解:移项,得![]()
两边平方,得![]()
即![]()
两边再平方,得![]()
即![]()
解这个方程得:![]()
检验:当![]() 时,原方程左边
时,原方程左边![]() ,右边
,右边![]()
![]() 不是原方程的根;
不是原方程的根;
当![]() 时,原方程左边
时,原方程左边![]() ,右边
,右边![]()
![]() 原方程的根
原方程的根
![]() 原方程的根是
原方程的根是![]() .
.
(1)请仿照上述解法,求出方程![]() 的解;
的解;
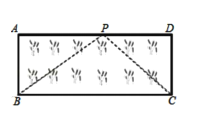
(2)如图已知矩形草坪![]() 的长
的长![]() ,宽
,宽![]() ,小华把一根长为
,小华把一根长为![]() 的绳子的一端固定在点
的绳子的一端固定在点![]() ,从草坪边沿
,从草坪边沿![]() 走到点
走到点![]() 处,把长绳
处,把长绳![]() 段拉直并固定在点
段拉直并固定在点![]() ,然后沿草坪边沿
,然后沿草坪边沿![]() 走到点
走到点![]() 处,把长绳剩下的一段拉直,长绳的另一端恰好落在点
处,把长绳剩下的一段拉直,长绳的另一端恰好落在点![]() ,则
,则![]()
![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】将一副三角尺(在![]() 中,
中,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() )如图摆放,点
)如图摆放,点![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() 经过点
经过点![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() (
(![]() ),
),![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为![]() ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
科目: 来源: 题型:
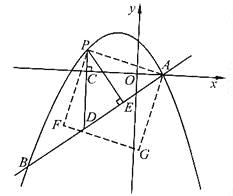
【题目】如图,在平面直角坐标系中,直线![]() 与抛物线
与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
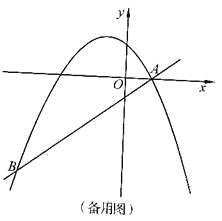
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,直接写出对应的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com