
科目: 来源: 题型:
【题目】综合与实践:
概念理解:将△ABC 绕点 A 按逆时针方向旋转,旋转角记为 θ(0°≤θ≤90°),并使各边长变为原来的 n 倍,得到△AB′C′,如图,我们将这种变换记为[θ,n],![]() :
:![]() .
.

问题解决:(2)如图,在△ABC 中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得到△AB′C′,使点 B,C,C′在同一直线上,且四边形 ABB′C′为矩形,求 θ 和 n 的值.

拓广探索:(3)在△ABC 中,∠BAC=45°,∠ACB=90°,对△ABC作变换 得到△AB′C′,则四边形 ABB′C′为正方形
查看答案和解析>>
科目: 来源: 题型:
【题目】某种商品每天的销售利润![]() 元,销售单价
元,销售单价![]() 元,间满足函数关系式:
元,间满足函数关系式:![]() ,其图象如图所示.
,其图象如图所示.
(1)销售单价为多少元时,该种商品每天的销售利润最大? 最大利润为多少元?
(2)销售单价在什么范围时,该种商品每天的销售利润不低于21 元?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点 A 和点 C 分别在x 轴和 y 轴的正半轴上,OA=6,OC=4,以 OA,OC 为邻边作矩形 OABC, 动点 M,N 以每秒 1 个单位长度的速度分别从点 A、C 同时出发,其中点 M 沿 AO 向终点 O 运动,点 N沿 CB 向终点 B 运动,当两个动点运动了 t 秒时,过点 N 作NP⊥BC,交 OB 于点 P,连接 MP.
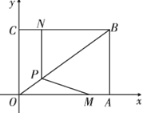
(1)直接写出点 B 的坐标为 ,直线 OB 的函数表达式为 ;
(2)记△OMP 的面积为 S,求 S 与 t 的函数关系式![]() ;并求 t 为何值时,S有最大值,并求出最大值.
;并求 t 为何值时,S有最大值,并求出最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F.

(1)求证:△APD≌△CPD;
(2)求证:△APE∽△FPA;
(3)若PE=2,EF=6,求PC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.
(1)t为何值时,△CPQ的面积等于△ABC面积的![]() ?
?
(2)运动几秒时,△CPQ与△CBA相似?
(3)在运动过程中,PQ的长度能否为1cm?试说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:四边形ADCF是菱形;
(3)若AC=5,AB=6,求菱形ADCF的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小明从中随机抽取一张卡片是足球社团B的概率是 .
(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.
查看答案和解析>>
科目: 来源: 题型:
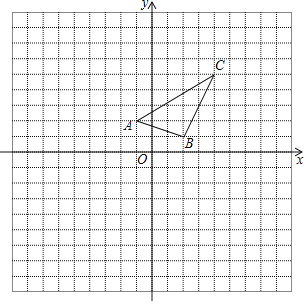
【题目】如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)以原点O为位似中心,在x轴的上方画出△A1B1C1,使△A1B1C1与△ABC位似,且相似比为2;
(2)△A1B1C1的面积是 平方单位.
(3)点P(a,b)为△ABC内一点,则在△A1B1C1内的对应点P’的坐标为 .
查看答案和解析>>
科目: 来源: 题型:
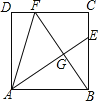
【题目】如图,正方形ABCD中,BE=FC,CF=2FD,AE、BF交于点G,连接AF,给出下列结论:①AE⊥BF; ②AE=BF; ③BG=![]() GE; ④S四边形CEGF=S△ABG,其中正确的个数为( )
GE; ④S四边形CEGF=S△ABG,其中正确的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
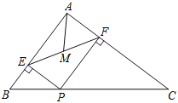
【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com