
科目: 来源: 题型:
【题目】在![]() 中,
中,![]() .
.
(1)观察猜想
如图1,![]() 分别交
分别交![]() 于点
于点![]()
![]() 的值是 ,直线
的值是 ,直线![]() 与直线
与直线![]() 相交所成的较小角的度数是 .
相交所成的较小角的度数是 .

(2)类比探究
如图2,将![]() 绕点
绕点![]() 逆时针旋转,请写出
逆时针旋转,请写出![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 相交所成的小角的度数,并就图2的情形说明理由,
相交所成的小角的度数,并就图2的情形说明理由,
(3)解决问题
若![]() ,请直接写出点
,请直接写出点![]() 在同一直线上时
在同一直线上时![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
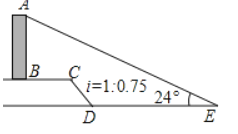
【题目】如图,![]() 是一垂直于水平面的建筑物,某同学从建筑物底端
是一垂直于水平面的建筑物,某同学从建筑物底端![]() 出发,先沿水平方向向右行走
出发,先沿水平方向向右行走![]() 米到达点
米到达点![]() 再经过段坡度(或坡比)为
再经过段坡度(或坡比)为![]() 坡长为
坡长为![]() 米的斜坡
米的斜坡![]() 到达点
到达点![]() 然后再沿水平方向向右行走
然后再沿水平方向向右行走![]() 米到达点
米到达点![]() 均在同一平面内).在
均在同一平面内).在![]() 处测得建筑物顶端
处测得建筑物顶端![]() 的仰角为
的仰角为![]() 求建筑物
求建筑物![]() 的高度. (参考数据:
的高度. (参考数据:![]() ,
,![]()
![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】在一次数学活动课上,某校初三数学老师带领学生去测河宽,如图所示,某学生在河东岸点![]() 处观测到河对岸水边有一点
处观测到河对岸水边有一点![]() ,测得
,测得![]() 在
在![]() 北偏西
北偏西![]() 的方向上,沿河岸向北前行20米到达
的方向上,沿河岸向北前行20米到达![]() 处,测得
处,测得![]() 在
在![]() 北偏西
北偏西![]() 的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈
的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈![]() ,sin31°≈
,sin31°≈![]() )
)

查看答案和解析>>
科目: 来源: 题型:
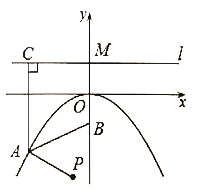
【题目】如图,抛物线![]() 经过点
经过点![]() .点
.点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 轴,点
轴,点![]() 是抛物线
是抛物线![]() 上一点,
上一点,![]() 于点
于点![]() .
.
![]() 求抛物线解析式:
求抛物线解析式:
![]() 在抛物线对称轴上是否存在一定点
在抛物线对称轴上是否存在一定点![]() ,使得
,使得![]() 永远成立?若存在,求出点
永远成立?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
![]() 若点
若点![]() 坐标为
坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程, 根据等式的基本性质,把方程转化为![]() 的形式;求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为二元一次方程组来解.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生不适合原方程的根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想-转化,即:把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程可以通过因式分解把它转化为
的形式;求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为二元一次方程组来解.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生不适合原方程的根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想-转化,即:把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程可以通过因式分解把它转化为![]() ,解方程
,解方程![]() 和
和![]() ,可得方程
,可得方程![]() 的解
的解
![]() 问题:方程
问题:方程![]() 的解是
的解是![]() ,
,![]() ,
,![]()
![]() 拓展:用“转化”思想求方程
拓展:用“转化”思想求方程![]() 的解;
的解;
![]() 变式:用“转化”思想解方程
变式:用“转化”思想解方程![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】为庆祝新中国成立七十周年,某校开展了“祖国在我心中”手抄报展评活动.小红同学设计的手抄报如右图所示,手抄报的外边框长![]() ,宽
,宽![]() ,正中央是一个与整个手抄报长宽比例相同的矩形.又知四周边衬所占面积是手抄报面积的四分之一,上、下边衬等宽,左、右边衬等宽,求小红设计手抄报的四周边衬的宽度. (精确到
,正中央是一个与整个手抄报长宽比例相同的矩形.又知四周边衬所占面积是手抄报面积的四分之一,上、下边衬等宽,左、右边衬等宽,求小红设计手抄报的四周边衬的宽度. (精确到![]() )
)
(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目: 来源: 题型:
【题目】(本题10分)如图,直线y=x+m和抛物线y=![]() +bx+c都经过点A(1,0),
+bx+c都经过点A(1,0),
B(3,2).
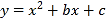
(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)
查看答案和解析>>
科目: 来源: 题型:
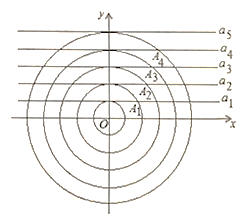
【题目】如图所示,在平面直角坐标系中,一组同心圆的圆心为坐标原点![]() ,它们的半径分别为
,它们的半径分别为![]() .按照“加
.按照“加![]() "依次递增; 一组平行线
"依次递增; 一组平行线![]() , ..分别过
, ..分别过![]() ,且与过该点的圆相切.若半径为
,且与过该点的圆相切.若半径为![]() 的圆与
的圆与![]() 在第一象限内交于点
在第一象限内交于点![]() ,半径为
,半径为![]() 的圆与
的圆与![]() 在第象限内相交于点
在第象限内相交于点![]() ,半径为
,半径为![]() 的圆与
的圆与![]() 在第一象限内相交于点
在第一象限内相交于点![]() 按照此规律,则点
按照此规律,则点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com