
科目: 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目: 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.

请你根据统计图解答下列问题:
(1)参加比赛的学生共有____名;
(2)在扇形统计图中,m的值为____,表示“D等级”的扇形的圆心角为____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目: 来源: 题型:
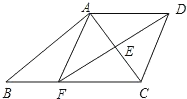
【题目】如图,已知:梯形ABCD中,AD∥BC,E为AC的中点,连接DE并延长交BC于点F,连接AF.
(1)求证:AD=CF;
(2)在原有条件不变的情况下,请你再添加一个条件(不再增添辅助线),使四边形AFCD成为菱形,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于M(1,3),N两点,点N的横坐标为﹣3.
的图象交于M(1,3),N两点,点N的横坐标为﹣3.

(1)根据图象信息可得关于x的方程![]() 的解为 ;
的解为 ;
(2)求一次函数的解析式.
查看答案和解析>>
科目: 来源: 题型:
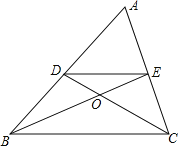
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE交CD于点O,连接DE,有下列结论:①DE=![]() BC;②△BOC∽△COE;③BO=2EO;④AO的延长线经过BC的中点.其中正确的是____.(填写所有正确结论的编号)
BC;②△BOC∽△COE;③BO=2EO;④AO的延长线经过BC的中点.其中正确的是____.(填写所有正确结论的编号)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将边长为1的正三角形OAP沿χ轴方向连续翻转若干次,点P依次落在点P1,P2,P3,…,P2018的位置,则点P2018的横坐标为( )
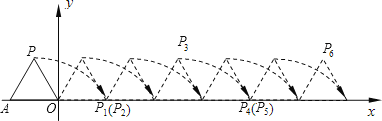
A.2016B.2017C.2018D.2019
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AO为Rt△ABC的角平分线,∠ACB=90°,以O为圆心,OC为半径的圆分别交AO,BC于点D,E,连接ED并延长交AC于点F.
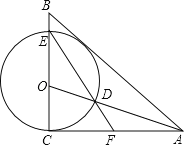
(1)求证:AB是⊙O的切线;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)在(2)的条件下,若⊙O的半径为4,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】一次函数![]() 的图象是直线
的图象是直线![]() ,点A(14,1)是
,点A(14,1)是![]() 与反比例函数y=
与反比例函数y=![]() 的图象的交点.
的图象的交点.
(1)一次函数与反比例函数的表达式;
(2)将直线![]() 平移后得直线
平移后得直线![]() ,与y轴正半轴交于点B(0,t),同时交
,与y轴正半轴交于点B(0,t),同时交![]() 轴于点C,若S△ABC=18,求t的值.
轴于点C,若S△ABC=18,求t的值.
查看答案和解析>>
科目: 来源: 题型:
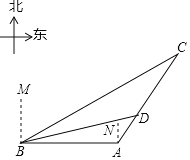
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)
查看答案和解析>>
科目: 来源: 题型:
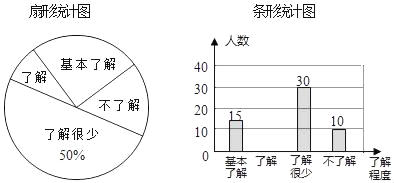
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应扇形的圆心角为 °;
(2)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为 人;
(3)若从对校园安全知识达到“了解”程度的3个女生A、B、C和2个男生M、N中分别随机抽取1人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到女生A的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com