
科目: 来源: 题型:
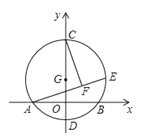
【题目】如图,以G(0,3)为圆心,半径为6的圆与x轴交于A.B两点,与y轴交于C,D两点,点E为⊙G上一动点,CF⊥AE于F,点E在⊙G的运动过程中,线段FG的长度的最小值为( )
A.![]() 1B.2
1B.2![]() -2C.3
-2C.3![]() D.3
D.3![]() 3
3
查看答案和解析>>
科目: 来源: 题型:
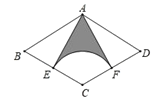
【题目】如图,在菱形ABCD中,点E是BC的中点,以C为圆心、CE为半径作弧,交CD于点F,连接AE、AF.若AB=2,∠B=60°,则阴影部分的面积为( )
A.![]()
![]() B.
B.![]()
![]()
C.2![]() –πD.2
–πD.2![]()
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】服装柜在销售中发现某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存.经市场调查发现,如果每件童装每降价4元,那么平均每天就可多售出8件,要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】按要求解方程:
(1)直接开平方法: 4(t-3)2=9(2t-3)2
(2)配方法:2x2-7x-4=0
(3)公式法: 3x2+5(2x+1)=0
(4)因式分解法:3(x-5)2=2(5-x)
(5)abx2-(a2+b2)x+ab=0 (ab≠0)
(6)用配方法求最值:6x2-x-12
查看答案和解析>>
科目: 来源: 题型:
【题目】(思考题)
阅读下面的情景对话,然后解答问题:
老师:我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
小华:等边三角形一定是奇异三角形;
小明:那直角三角形是否存在奇异三角形呢?
(1)①根据“奇异三角形”的定义,小红得出命题:“等边三角形一定是奇异三角形”,请判断小红提出的命题是否正确,并填空:命题 (填“正确”或“不正确”),不要说嘛理由.
②若某三角形的三边长分别是2、4、![]() ,则△ABC是奇异三角形吗? (填“是”或“不是”),不要说嘛理由.
,则△ABC是奇异三角形吗? (填“是”或“不是”),不要说嘛理由.
(2)在Rt△ABC中,两边长分别是a=5![]() 、c=10,这个三角形是否是奇异三角形?请说明理由.
、c=10,这个三角形是否是奇异三角形?请说明理由.
(3)在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了节省材料,某农户利用一段墙体为一边(墙体的长为10米),用总长为40m的围网围成如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.

(1)求AE:EB的值;
(2)当BE的长为何值时,长方形ABCD的面积达到72m2?
(3)当BE的长为何值时,矩形区域①的面积达到最大值?并求出其最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目: 来源: 题型:
【题目】服装柜在销售中发现某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存.经市场调查发现,如果每件童装每降价4元,那么平均每天就可多售出8件,要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC的三边长分别为a、b、c,下列条件:①∠B=∠C-∠A; ②a2=(b+c)(b-c);③∠A:∠B:∠C=3:4:5;④a:b:c=5:12:13, 其中能判断△ABC是直角三角形的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com