
科目: 来源: 题型:
【题目】桑桑同学利用寒假30天的时间贩卖草莓,某品种草莓的成本为10元/千克,该品种草莓在第![]() 天的销售量与销售单价如下表:
天的销售量与销售单价如下表:
销售量 |
|
销售单价 | 当 |
当 |
(1)请计算第几天该品种草莓的销售单价为25元/千克?
(2)这30天中,该同学第几天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】为了方便游客观赏景点,某景区设计建造了如图所示的高为6米的观景台![]() ,且坡面
,且坡面![]() 的坡度比为1:1.后来为了方便行人推车(如子女带老人旅游等),决定降低坡度,新坡面的坡度比为
的坡度比为1:1.后来为了方便行人推车(如子女带老人旅游等),决定降低坡度,新坡面的坡度比为![]() .
.
(1)求新坡面的坡角![]() .
.
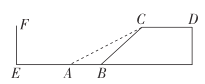
(2)原坡面底部的正前方13米(![]() 的长)有一座古建筑
的长)有一座古建筑![]() ,为保护文物,当地文物管理部门规定,坡面底部至少距古建筑7米,请问新的设计方案能否通过,试说明理由.(参考数据:
,为保护文物,当地文物管理部门规定,坡面底部至少距古建筑7米,请问新的设计方案能否通过,试说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
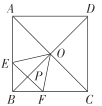
【题目】如图,在边长为2的正方形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 是
是![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() ,分别交正方形的两条边于点
,分别交正方形的两条边于点![]() ,
,![]() ,连接
,连接![]() 、
、![]() ,设
,设![]() ,
,![]() 的面积为
的面积为![]() ,则能大致反映
,则能大致反映![]() 与
与![]() 之间的函数关系的图象为( )
之间的函数关系的图象为( )
A.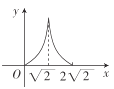 B.
B.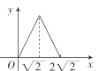 C.
C. D.
D.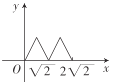
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为
x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为![]() m.
m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?

查看答案和解析>>
科目: 来源: 题型:
【题目】某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx﹣75.其图象如图.
(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
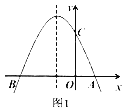

(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上是否存在点![]() ,使得
,使得![]() 的周长最小?若存在,求出点
的周长最小?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2013年,某市某楼盘以每平方米4000元的均价对外销售.因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2015年的均价为每平方米3240元.
(1)求平均每年下调的百分率;
(2)假设2016年的均价仍然下调相同的百分率,李明准备购买一套100平方米的住房,他持有现金10万元,可以在银行贷款20万元,李明的愿望能否实现(房价每平方米按照均价计算)?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且对称轴为直线
点,且对称轴为直线![]() ,点
,点![]() 坐标为
坐标为![]() .则下面的四个结论:①
.则下面的四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 或
或![]() .其中正确的是( )
.其中正确的是( )

A.①②B.①③C.①④D.②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com