
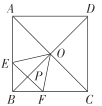
【题目】如图,在边长为2的正方形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 是
是![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() ,分别交正方形的两条边于点
,分别交正方形的两条边于点![]() ,
,![]() ,连接
,连接![]() 、
、![]() ,设
,设![]() ,
,![]() 的面积为
的面积为![]() ,则能大致反映
,则能大致反映![]() 与
与![]() 之间的函数关系的图象为( )
之间的函数关系的图象为( )
A.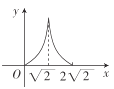 B.
B.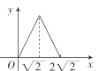 C.
C. D.
D.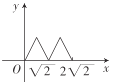
【答案】C
【解析】
分析题意,由正方形的性质得![]() ,然后得到EF与x的关系,他们的关系分两种情况,依情况来判断抛物线的开口方向.
,然后得到EF与x的关系,他们的关系分两种情况,依情况来判断抛物线的开口方向.
解:∵四边形ABCD是正方形,边长为2,
∴AC=BD=![]() ,OB=OD=
,OB=OD=![]() BD=
BD=![]() ,
,
①当P在OB上时,即0≤x≤![]() ,
,
∵EF∥AC,
∴△BEF∽△BAC,
∴EF:AC=BP:OB,
∴EF=2BP=2x,
∵![]() ,
,
∴![]() ;
;
②当P在OD上时,即![]() <x≤
<x≤![]() ,
,
∵EF∥AC,
∴△DEF∽△DAC,
∴EF:AC=DP:OD,
即EF:![]() =(
=(![]() ):
):![]() ,
,
∴![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
这是一个二次函数,根据二次函数的性质可知:
二次函数的图象是一条抛物线,开口方向取决于二次项的系数.
当系数>0时,抛物线开口向上;系数<0时,开口向下.
故选:C.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】为了落实国务院的指示精神,地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:![]() . 设这种产品每天的销售利润为w元.
. 设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
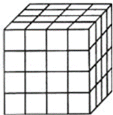
【题目】如图,把一个木制正方体的表面涂上颜色,然后将正方体分割成64个大小相同的小正方体.从这些小正方体中任意取出一个,求取出的小正方体:
(1)三面涂有颜色的概率;
(2)两面涂有颜色的概率;
(3)各个面都没有颜色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年,某市某楼盘以每平方米4000元的均价对外销售.因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2015年的均价为每平方米3240元.
(1)求平均每年下调的百分率;
(2)假设2016年的均价仍然下调相同的百分率,李明准备购买一套100平方米的住房,他持有现金10万元,可以在银行贷款20万元,李明的愿望能否实现(房价每平方米按照均价计算)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,点A的坐标为(9,6),AB⊥y轴,垂足为B,点P从原点O出发向x轴正方向运动,同时,点Q从点A出发向点B运动,当点Q到达点B时,点P、Q同时停止运动,若点P与点Q的速度之比为1:2,则下列说法正确的是( )
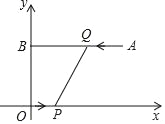
A. 线段PQ始终经过点(2,3)
B. 线段PQ始终经过点(3,2)
C. 线段PQ始终经过点(2,2)
D. 线段PQ不可能始终经过某一定点
查看答案和解析>>
科目:初中数学 来源: 题型:
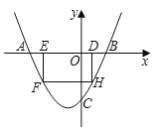
【题目】如图,抛物线![]() 与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
(1)求抛物线的解析式;
(2)当矩形 DEFH 的周长最大时,求矩形 DEFH 的面积;
(3)在(2)的条件下,矩形 DEFH 不动,将抛物线沿着 x 轴向左平移 m 个单位,抛物线与矩形 DEFH的边交于点 M、N,连接 M、N.若 MN 恰好平分矩形 DEFH 的面积,求 m 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、P、B、C是⊙O上四点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形;
(2)连接OA,OB,当点P位于什么位置时,四边形PBOA是菱形?并说明理由;
(3)已知PA=a,PB=b,求PC的长(用含a和b的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011广西崇左,18,3分)已知:二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+b<m(am+b)(m≠1的实数);④(a+c)2<b2;⑤a>1.其中正确的项是( )
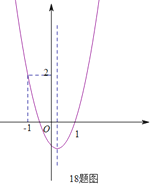
A. ①⑤ B. ①②⑤ C. ②⑤ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com