
科目: 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,以
,以![]() 为直径的半圆
为直径的半圆![]() 在矩形
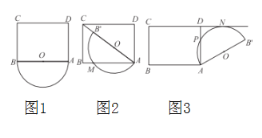
在矩形![]() 的外部,如图1,将半圆
的外部,如图1,将半圆![]() 绕点
绕点![]() 顺时针旋转α度(0°≤ɑ≤180°).
顺时针旋转α度(0°≤ɑ≤180°).
(1)在旋转过程中,![]() 的最小值是_____________,当半圆
的最小值是_____________,当半圆![]() 的直径落在对角线
的直径落在对角线![]() 上时,如图2,设半圆
上时,如图2,设半圆![]() 与
与![]() 的交点为
的交点为![]() ,则
,则![]() 长为__________.
长为__________.
(2)将半圆![]() 与直线
与直线![]() 相切时,切点为
相切时,切点为![]() ,半圆
,半圆![]() 与线段
与线段![]() 的交点为
的交点为![]() ,如图3,求劣弧
,如图3,求劣弧![]() 的长;
的长;
(3)在旋转过程中,当半圆弧与直线![]() 只有一个交点时,设此交点与点
只有一个交点时,设此交点与点![]() 的距离为
的距离为![]() 请直接写出
请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
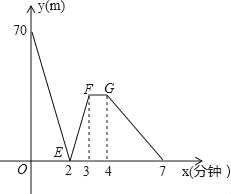
【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与他们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是 米,甲机器人前2分钟的速度为 米/分;
(2)若前3分钟甲机器人的速度不变,求线段EF所在直线的函数解析式;
(3)若线段FG∥x轴,则此段时间,甲机器人的速度为 米/分;
(4)求A、C两点之间的距离;
(5)若前3分钟甲机器人的速度不变,直接写出两机器人出发多长时间相距28米.
查看答案和解析>>
科目: 来源: 题型:
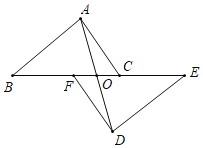
【题目】如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于O.
(1)求证:△ABC≌△DEF;
(2)求证:AD与BE互相平分;
(3)若BF=5,FC=4,直接写出EO的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一节数学活动课上,王老师将本班学生身高数据(精确到1厘米)出示给大家,要求同学们各自独立绘制一幅频数分布直方图,甲绘制的如图①所示,乙绘制的如图②所示,经王老师批改,甲绘制的图是正确的,乙在数据整理与绘图过程中均有个别错误.
(1)写出乙同学在数据整理或绘图过程中的错误(写出一个即可);
(2)甲同学在数据整理后若用扇形统计图表示,则159.5﹣164.5这一部分所对应的扇形圆心角的度数为 ;
(3)该班学生的身高数据的中位数是 ;
(4)假设身高在169.5﹣174.5范围的5名同学中,有2名女同学,班主任老师想在这5名同学中选出2名同学作为本班的正、副旗手,那么恰好选中一名男同学和一名女同学当正,副旗手的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,所有正三角形的一边平行于![]() 轴,一顶点在
轴,一顶点在![]() 轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用
轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用![]() 表示,其中
表示,其中![]() 与
与![]() 轴、底边
轴、底边![]() 与
与![]() 与
与![]() 、…均相距一个单位,则顶点
、…均相距一个单位,则顶点![]() 的坐标是__________,
的坐标是__________,![]() 的坐标是__________.
的坐标是__________.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等边三角形![]() 边长是定值,点
边长是定值,点![]() 是它的外心,过点
是它的外心,过点![]() 任意作一条直线分别交
任意作一条直线分别交![]() 于点
于点![]() ,将
,将![]() 沿直线
沿直线![]() 折叠,得到
折叠,得到![]() ,若
,若![]() 分别交
分别交![]() 于点
于点![]() ,连接
,连接![]() ,则下列判断错误的是( )
,则下列判断错误的是( )
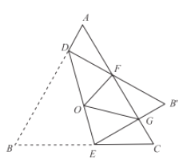
A.△![]() ≌△
≌△![]()
B.![]() 的周长是一个定值
的周长是一个定值
C.四边形![]() 的面积是一个定值
的面积是一个定值
D.四边形![]() 的面积是一个定值
的面积是一个定值
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于()
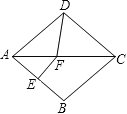
A.50°B.60°C.70°D.80°
查看答案和解析>>
科目: 来源: 题型:
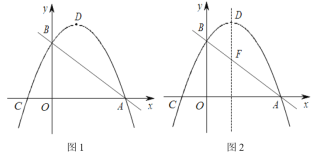
【题目】如图1,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点B;抛物线
与x轴交于点A,与y轴交于点B;抛物线![]() (a≠0)过A,B两点,与x轴交于另一点C(-1,0),抛物线的顶点为D.
(a≠0)过A,B两点,与x轴交于另一点C(-1,0),抛物线的顶点为D.
(1)求抛物线的解析式;
(2)在直线AB上方的抛物线上有一动点E,求出点E到直线AB的距离的最大值;
(3)如图2,直线AB与抛物线的对称轴相交于点F,点P在坐标轴上,且点P到直线 BD,DF的距离相等,请直接写出点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以
上一动点,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,点
,点![]() 的位置随点
的位置随点![]() 的位置变化而变化.
的位置变化而变化.
(1)如图1,当点![]() 在菱形
在菱形![]() 内部或边上时,连接
内部或边上时,连接![]() ,
,![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;
(2)当点![]() 在菱形
在菱形![]() 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3) 如图4,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】(2019·济源一模)为支持国家南水北调工程建设,小王家由原来养殖户变为种植户, 经市场调查得知,种植草莓不超过20亩时,所得利润 y(元)与种植面积 m(亩)满足关系式y=1500 m;超过20亩时,y=1380m+2400.而当种植樱桃的面积不超过15亩时,每亩可获得利润1800元;超过15亩时,每亩获得利润z(元)与种植面积x(亩)之间的函数关系式为z=-20x+2 100.
(1)设小王家种植x亩樱桃所获得的利润为P元,直接写出P关于x的函数关系式,并写出自变量的取值范围;
(2)如果小王家计划承包40亩荒山种植草莓和樱桃,当种植樱桃面积(x亩)满足0<x<20时,求小王家总共获得的利润w(元)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com