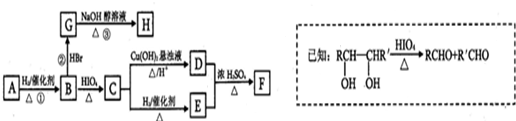
分析:(1)由图象计算C的浓度变化,再根据v=
计算反应速率;
(2)t
4~t
5阶段正逆反应速率减小且相等,如是降低温度,平衡移动发生移动,则正逆反应速率不相等;根据C、A浓度的变化判断二者计量数关系,根据t
4~t
5阶段判断化学方程式;由图2可知t
2时增大了某一物质的浓度,已知t
2-t
3阶段,C的体积分数变小,则增大了B的浓度,根据平衡移动来判断正逆反应速率的关系;
(3)根据A的浓度变化,利用化学方程式计算出B的浓度变化,由平衡时的浓度,再求出起始的浓度和物质的量;
(4)根据图象中平衡时各物质的浓度,计算平衡常数;
(5)计算3molA反应的热量,结合方程式书写热化学方程式;
(6)t
2时刻后图象变化如图3图4,由图可知,某一速率增加、另一速率减小,必须保证A浓度增大的同时B、C浓度减小,或者A浓度减小的同时B、C浓度增大.
解答:
解:(1)若t
1=15s,生成物C在t
0~t
1时间段的平均反应速率为:v=
=0.004mol?L
-1?s
-1,
故答案为:0.004;
(2)t
3~t
4阶段与t
4~t
5阶段正逆反应速率都相等,而t
3~t
4阶段为使用催化剂,如t
4~t
5阶段改变的条件为降低反应温度,平衡移动发生移动,则正逆反应速率不相等,则t
4~t
5阶段应为减小压强;反应中A的浓度变化为0.15mol/L-0.06mol/L=0.09mol/L,C的浓度变化为0.11mol/L-0.05mol/L=0.06mol/L,反应中A与C的计量数之比为0.09:0.06=3:2,则该反应中气体的化学计量数之和前后相等,则有:3A(g)?B(g)+2C(g),
由图2可知t
2时增大了某一物质的浓度,已知t
2-t
3阶段,C的体积分数变小,则增大了B的浓度,增大B的浓度平衡向逆方向移动,所以v正小于v逆;
故答案为:小于;
(3)根据方程式可知消耗0.09mol/L的A,则生成0.03mol/L的B,容器的体积为
=2L,生成B的物质的量为0.03mol/L×2L=0.06mol,平衡时B的物质的量为0.05mol/L×2L=0.1mol,所以起始时B的物质的量为0.1mol-0.06mol=0.04mol,
故答案为:0.04;
(4)由图象可知t
1时刻,各物质的平衡浓度为c(A)=0.06mol/L,c(B)=0.05mol/L,c(C)=0.11mol/L,则K=
=
=2.8;
故答案为:2.8;
(5)反应的方程式为3A(g)?B(g)+2C(g),A的物质的量减少0.03mol,而此过程中容器与外界的热交换总量为akJ,则A的物质的量减少3mol,与外界的热交换总量为100akJ,由图象可知t
5~t
6阶段应为升高温度,A的物质的量减少,说明向正反应方向移动,则正反应吸热,该反应的热化学方程式为3A(g)

B(g)+2C(g)△H=+100akJ?mol
-1,
故答案为:3A(g)?B(g)+2C(g)△H=+100akJ?mol
-1;
(6)t
2时刻后图象变化如图3图4,由图可知,某一速率增加、另一速率减小,必须保证A浓度增大的同时B、C浓度减小,或者A浓度减小的同时B、C浓度增大,已知原来起始时n(A)=0.3mol,n(B)=0.1-0.06mol=0.04mol,n(C)=0.1mol,采用极限法转化反应物或生成物的量,如果与原来相同则正确,
a.恒温恒压下,按照2:1比例充入任意量的B和C,转化部分B、C不能得到,n(A)=0.3mol,n(B)=0.04mol,n(C)=0.1mol,故a错误;
b.恒温恒压下,加入0.24mol A、0.06mol B和0.14mol C,转化部分B、C能得到,n(A)=0.3mol,n(B)=0.04mol,n(C)=0.1mol,故b正确;
c.恒温恒压下,加入0.12mol A、0.1mol B和0.22mol C,转化部分B、C不能得到,n(A)=0.3mol,n(B)=0.04mol,n(C)=0.1mol,故c错误;
d.恒温恒压下,加入0.14mol B和0.30mol C,转化部分B、C能得到,n(A)=0.3mol,n(B)=0.04mol,n(C)=0.1mol,故d正确;
故答案为:bd.

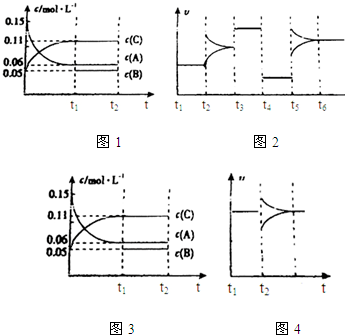
 B(g)+2C(g)△H=+100akJ?mol-1,
B(g)+2C(g)△H=+100akJ?mol-1,

 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案 实验室制配0.5mol/L的NaOH溶液500mL.
实验室制配0.5mol/L的NaOH溶液500mL.