
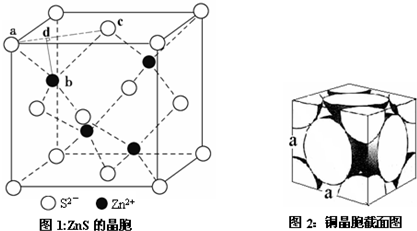
分析 (1)硫化锌的晶胞类似于金刚石的晶胞,每个锌离子和四个硫离子形成正四面体结构,则∠abc=109°28′;
(2)根据图知,每个硫离子连接4个锌离子;
(3)1pm=10-12 m;
(4)每个黑色小球连接4个白色小球,构成正四面体结构,白球和黑球之间的夹角为109°28′,两个白球之间的距离=270$\sqrt{2}$pm,则白球之间距离的一半为135$\sqrt{2}$pm,135$\sqrt{2}$pm对应的夹角为$\frac{109°28′}{2}$,根据正弦定理计算a位置S2-离子与b位置Zn2+离子之间的距离;
(5)①该晶胞是面心立方晶胞,在晶胞中铜原子的配位数=12×4÷2,铜晶胞的堆积模型的名称是面心立方最密堆积;
②对角线上的原子紧密相连,晶胞对角线长度=4r=$\sqrt{2}$a nm;
③该晶胞中Cu原子个数=8×$\frac{1}{8}$+6×$\frac{1}{2}$=4,则四个Cu原子体积=4×$\frac{4}{3}$πr3,晶胞体积=(a nm)3,
空间利用率=$\frac{4个铜原子体积之和}{晶胞体积}×100%$.
解答 解:(1)硫化锌的晶胞类似于金刚石的晶胞,每个锌离子和四个硫离子形成正四面体结构,则∠abc=109°28′,故答案为:109°28′;
(2)根据图知,以c离子为例,在该晶胞中c离子连接2个锌离子,在上一个晶胞中连接2个锌离子,所以每个硫离子连接4个锌离子,则硫离子的配位数是4,故答案为:4;
(3)1pm=10-12 m,故答案为:10-12;
(4)每个黑色小球连接4个白色小球,构成正四面体结构,白球和黑球之间的夹角为109°28′,两个白球之间的距离=270$\sqrt{2}$pm,则白球之间距离的一半为135$\sqrt{2}$pm,135$\sqrt{2}$pm对应的夹角为$\frac{109°28′}{2}$,根据正弦定理计算a位置S2-离子与b位置Zn2+离子之间的距离=$\frac{135\sqrt{2}}{sin\frac{109°28′}{2}}$×10-10cm,
故答案为:$\frac{135\sqrt{2}}{sin\frac{109°28′}{2}}$×10-10;
(5)①该晶胞是面心立方晶胞,在晶胞中铜原子的配位数=12×4÷2=12,铜晶胞的堆积模型的名称是面心立方最密堆积,故答案为:12;面心立方密堆积;
②对角线上的原子紧密相连,晶胞对角线长度=4r=$\sqrt{2}$a nm,则r=$\frac{\sqrt{2}a}{4}$nm,故答案为:$\frac{\sqrt{2}a}{4}$;
③该晶胞中Cu原子个数=8×$\frac{1}{8}$+6×$\frac{1}{2}$=4,则四个Cu原子体积=4×$\frac{4}{3}$πr3=4×$\frac{4}{3}$π($\frac{\sqrt{2}a}{4}$nm)3,
晶胞体积=(a nm)3,
空间利用率=$\frac{4个铜原子体积之和}{晶胞体积}×100%$=$\frac{4×\frac{4}{3}×π×(\frac{\sqrt{2}}{4}anm)^{3}}{{(anm)}^{3}}×100%$=74%,
故答案为:74.
点评 本题考查晶胞计算,为高频考点,侧重考查学生分析计算及空间想象能力,明确晶胞中原子排列方式是解本题关键,难点是空间利用率的计算,空间利用率等于原子的体积与晶胞体积之比.


科目:高中化学 来源: 题型:选择题
| X | Y | |
| Z | W |
| A. | 元素W位于第三周期第ⅤA族 | |
| B. | 元素Y的氢化物水溶液呈酸性 | |
| C. | 元素X、Z的各种氯化物分子中,各原子均满足8电子稳定结构 | |
| D. | 元素X与氢元素形成的原子个数比为1:1的化合物有多种 |
查看答案和解析>>
科目:高中化学 来源: 题型:解答题
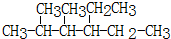 2,3-二甲基-3-乙基己烷
2,3-二甲基-3-乙基己烷 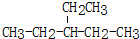 2-乙基戊烷
2-乙基戊烷查看答案和解析>>
科目:高中化学 来源: 题型:实验题
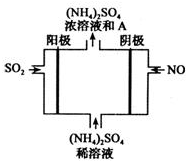 经研究发现,含pM2.5的雾霾主要成分有SO2、NOx、CxHy,及可吸入颗粒等.
经研究发现,含pM2.5的雾霾主要成分有SO2、NOx、CxHy,及可吸入颗粒等.查看答案和解析>>
科目:高中化学 来源: 题型:实验题
查看答案和解析>>
科目:高中化学 来源: 题型:推断题
查看答案和解析>>
科目:高中化学 来源: 题型:选择题
| A. | 不同种元素的原子 | B. | 不同种分子 | ||
| C. | 一种是分子,另一种是离子 | D. | 一种是分子,另一种是原子 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com