已知实数x,y满足x≥1,y≥1,(logax)2+(logay)2=loga(ax2)+loga(ay2),当a>1时,求loga(xy)的取值范围.
解:∵x≥1,y≥1,a>1,
∴(log
ax)
2+(log
ay)
2=log
a(ax
2)+log
a(ay
2)可变形为
(log
ax)
2+(log
ay)
2=log
aa+2log
ax+log
aa+2log
ay,
即(log
ax)
2+(log
ay)
2-2log
ax-2log
ay-2=0,
即(log
ax+log
ay)
2-2log
ax•log
ay-2(log
ax+log
ay)-2=0
设log
ax=m,log
ay=n,则m≥0,n≥0,且(m+n)
2-2mn-2(m+n)-2=0
∵mn≤(

)
2=
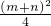
∴(m+n)
2-2mn-2(m+n)-2=0≥(m+n)
2-2×
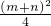
-2(m+n)-2
即(m+n)
2-4(m+n)-4≤0
∴2-2

≤m+n≤2+2

即2-2

≤log
ax+log
ay≤2+2

即2-2

≤log
a(xy)≤2+2

又x≥1,y≥1,a>1,可得0≤log
a(xy)
所以0≤log
a(xy)≤2+2

分析:先利用对数运算性质将已知对数等式变形为关于log
ax,log
ay的等式,再利用换元法及均值定理将等式转化为不等式,解不等式即可得所求范围
点评:本题考查了对数运算性质,利用均值定理化等式为不等式求变量范围的解题技巧,转化化归的思想方法

 )2=
)2=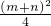
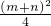 -2(m+n)-2
-2(m+n)-2 ≤m+n≤2+2
≤m+n≤2+2
 ≤logax+logay≤2+2
≤logax+logay≤2+2
 ≤loga(xy)≤2+2
≤loga(xy)≤2+2



 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案