
【题目】在直角梯形![]() (如图1),
(如图1),![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 中点.将
中点.将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到几何体
,得到几何体![]() (如图2).
(如图2).
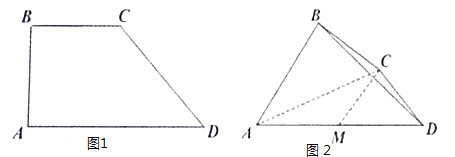
(1)求证:![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值.
的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)通过计算结合勾股定理的逆定理可以证明![]() ,再根据面面垂直的性质定理进行证明即可;
,再根据面面垂直的性质定理进行证明即可;
(2)法一、
取![]() 的中点
的中点![]() 连接
连接![]() ,根据
,根据![]() ,结合三棱锥的体积公式进行求解即可;
,结合三棱锥的体积公式进行求解即可;
法二、
取![]() 的中点
的中点![]() 连接
连接![]() ,由题设可知
,由题设可知![]() 为等腰直角三角形,所以
为等腰直角三角形,所以![]() 面
面![]() ,连接
,连接![]() ,因为
,因为![]() 分别为
分别为![]() 和
和![]() 的中点,所以
的中点,所以![]() ,由(1)可知
,由(1)可知![]() ,故以
,故以![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,如图所示.运用向量法求解即可.
轴建立空间直角坐标系,如图所示.运用向量法求解即可.
解:(1)由题设可知![]() ,
,![]() ,
,![]()
∴![]() ∴
∴![]()
又∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
∴![]() 面
面![]() .
.
(2)法一、等体积法
取![]() 的中点
的中点![]() 连接
连接![]() ,由题设可知
,由题设可知![]() 为等腰直角三角形,所以
为等腰直角三角形,所以![]() 面
面![]()
∵![]() 且
且![]()
而![]()
∴![]() 到面
到面![]() 的距离
的距离![]() ,
,
所以![]() .
.
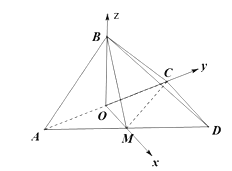
法二、向量法
取![]() 的中点
的中点![]() 连接
连接![]() ,由题设可知
,由题设可知![]() 为等腰直角三角形,所以
为等腰直角三角形,所以![]() 面
面![]() ,连接
,连接![]() ,因为
,因为![]() 分别为
分别为![]() 和
和![]() 的中点,所以
的中点,所以![]() ,由(1)可知
,由(1)可知![]() ,故以
,故以![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,如图所示.
轴建立空间直角坐标系,如图所示.
则![]() ,
,![]() ,
,![]() ,
,![]()
∴![]()
![]()
![]()
∴面![]() 的一个法向量
的一个法向量![]()
∴![]()


科目:高中数学 来源: 题型:
【题目】如图,已知矩形ABCD所在平面垂直直角梯形ABPE所在的平面于直线AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.
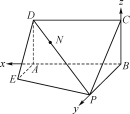
(1)求平面PCD与平面ABPE所成的二面角的余弦值;
(2)在线段PD上是否存在一点N,使得直线BN与平面PCD所成角的正弦值等于![]() ?若存在,试确定点N的位置;若不存在,请说明理由.
?若存在,试确定点N的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱柱![]() 中,
中,![]() 为
为![]() 的中点,点
的中点,点![]() 在侧棱
在侧棱![]() 上,
上,![]() 平面
平面![]()
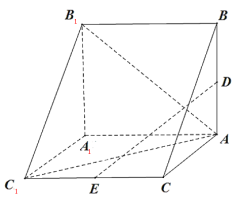
(1) 证明:![]() 是
是![]() 的中点;
的中点;
(2) 设![]() ,四边形
,四边形![]() 为边长为4正方形,四边形
为边长为4正方形,四边形![]() 为矩形,且异面直线
为矩形,且异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,求该三棱柱
,求该三棱柱![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着银行业的不断发展,市场竞争越来越激烈,顾客对银行服务质量的要求越来越高,银行为了提高柜员员工的服务意识,加强评价管理,工作中让顾客对服务作出评价,评价分为满意、基本满意、不满意三种.某银行为了比较顾客对男女柜员员工满意度评价的差异,在下属的四个分行中随机抽出40人(男女各半)进行分析比较.对40人一月中的顾客评价“不满意”的次数进行了统计,按男、女分为两组,再将每组柜员员工的月“不满意”次数分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如下频数分布表.
,得到如下频数分布表.
分组 |
|
|
|
|
|
女柜员 | 2 | 3 | 8 | 5 | 2 |
男柜员 | 1 | 3 | 9 | 4 | 3 |
(1)在答题卡所给的坐标系中分别画出男、女柜员员工的频率分布直方图;分别求出男、女柜员员工的月平均“不满意”次数的估计值,试根据估计值比较男、女柜员员工的满意度谁高?
(2)在抽取的40名柜员员工中:从“不满意”次数不少于20的员工中随机抽取3人,并用X表示随机抽取的3人中女柜员工的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午假期即将到来,永辉超市举办“浓情端午高考加油”有奖促销活动,凡持高考准考证考生及家长在端年节期间消费每超过600元(含600元),均可抽奖一次,抽奖箱里有10个形状、大小完全相同的小球(其中红球有3个,黑球有7个),抽奖方案设置两种,顾客自行选择其中的一种方案.

方案一:
从抽奖箱中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:
从抽奖箱中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.每次摸取1球,连摸3次,每摸到1次
(1)若小南、小开均分别消费了600元,且均选择抽奖方案一,试求他们均享受免单优惠的概率;
(2)若小杰消费恰好满1000元,试比较说明小杰选择哪一种抽奖方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东西向的铁路上有两个道口![]() 、
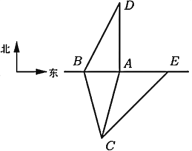
、![]() ,铁路两侧的公路分布如图,
,铁路两侧的公路分布如图,![]() 位于
位于![]() 的南偏西
的南偏西![]() ,且位于
,且位于![]() 的南偏东
的南偏东![]() 方向,
方向,![]() 位于
位于![]() 的正北方向,
的正北方向,![]() ,
,![]() 处一辆救护车欲通过道口前往
处一辆救护车欲通过道口前往![]() 处的医院送病人,发现北偏东
处的医院送病人,发现北偏东![]() 方向的
方向的![]() 处(火车头位置)有一列火车自东向西驶来,若火车通过每个道口都需要
处(火车头位置)有一列火车自东向西驶来,若火车通过每个道口都需要![]() 分钟,救护车和火车的速度均为
分钟,救护车和火车的速度均为![]() .
.
(1)判断救护车通过道口![]() 是否会受火车影响,并说明理由;
是否会受火车影响,并说明理由;
(2)为了尽快将病人送到医院,救护车应选择![]() 、
、![]() 中的哪个道口?通过计算说明.
中的哪个道口?通过计算说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com