
【题目】如图,已知矩形ABCD所在平面垂直直角梯形ABPE所在的平面于直线AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.
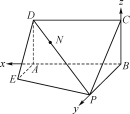
(1)求平面PCD与平面ABPE所成的二面角的余弦值;
(2)在线段PD上是否存在一点N,使得直线BN与平面PCD所成角的正弦值等于![]() ?若存在,试确定点N的位置;若不存在,请说明理由.
?若存在,试确定点N的位置;若不存在,请说明理由.
【答案】(1)![]() .(2)存在,当N在点D处时,直线BN与平面PCD所成角的正弦值等于
.(2)存在,当N在点D处时,直线BN与平面PCD所成角的正弦值等于![]() .
.
【解析】
(1)先根据题意建立空间直角坐标系,先求平面PCD的一个法向量,易知平面ABPE的一个法向量,再利用面面角的向量方法求解.
(2)假设线段PD上存在点N,设![]() =λ
=λ![]() ,则有
,则有![]() =
=![]() +
+![]() =(2λ,2-2λ,λ),再根据直线BN与平面PCD所成角α满足sinα=
=(2λ,2-2λ,λ),再根据直线BN与平面PCD所成角α满足sinα=![]() .由sinα=|cos〈
.由sinα=|cos〈![]() ,
,![]() 〉|=
〉|=![]() =
=![]() 即
即![]() =
=![]() 求解.
求解.
(1) 由AE⊥AB,且AE∥BP,得BP⊥AB.所以∠CBP是直二面角C-AB-P的平面角.
以![]() 为正交基底,建立空间直角坐标系Bxyz.
为正交基底,建立空间直角坐标系Bxyz.
B(0,0,0),A(2,0,0),P(0,2,0),E(2,1,0),C(0,0,1),D(2,0,1).
![]() =(0,-2,1),
=(0,-2,1),![]() =(2,0,0).
=(2,0,0).
设平面PCD的一个法向量为![]() =(a,b,c),
=(a,b,c),
由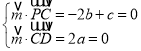 ,不妨取
,不妨取![]() =(0,1,2).
=(0,1,2).
易知平面ABPE的一个法向量为![]() =(0,0,1).
=(0,0,1).
设平面PCD与平面ABPE所成的二面角的大小为θ,
则由图可知θ∈![]() .
.
cosθ=|cos〈![]() ,
,![]() 〉|=
〉|=![]() =
=![]() .
.
所以平面PCD与平面ABPE所成的二面角的余弦值为![]() .
.
(2) 假设线段PD上存在点N,使得直线BN与平面PCD所成角α满足sinα=![]() .
.
即sinα=|cos〈![]() ,
,![]() 〉|=
〉|=![]() =
=![]() .
.
设![]() =λ
=λ![]() =λ(2,-2,1),其中λ∈[0,1].
=λ(2,-2,1),其中λ∈[0,1].
![]() =
=![]() +
+![]() =(2λ,2-2λ,λ).
=(2λ,2-2λ,λ).
由(1)知平面PCD的一个法向量![]() =(0,1,2),
=(0,1,2),
所以![]() =
=![]() ,
,
即9λ2-8λ-1=0,
解得λ=1或λ=![]() (舍去).
(舍去).
以当N在点D处时,直线BN与平面PCD所成角的正弦值等于![]() .
.


科目:高中数学 来源: 题型:
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为该椭圆的一条垂直于
为该椭圆的一条垂直于![]() 轴的动弦,直线
轴的动弦,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)证明:点![]() 恒在椭圆
恒在椭圆![]() 上.
上.
(2)设直线![]() 与椭圆
与椭圆![]() 只有一个公共点
只有一个公共点![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,在平面内是否存在定点
,在平面内是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出该点坐标;若不存在,说明理由.
恒成立?若存在,求出该点坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() ,过对角线
,过对角线![]() 作平面
作平面![]() 交棱
交棱![]() 于点E,交棱
于点E,交棱![]() 于点F,则:
于点F,则:
①四边形![]() 一定是平行四边形;
一定是平行四边形;
②四边形![]() 有可能为正方形;
有可能为正方形;
③四边形![]() 在底面
在底面![]() 内的投影一定是正方形;
内的投影一定是正方形;
④平面![]() 有可能垂直于平面
有可能垂直于平面![]() .
.
其中所有正确结论的序号为( )
A.①②B.②③④C.①④D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为3的正方体ABCDA1B1C1D1中,A1E=CF=1.
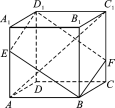
(1)求异面直线AC1与D1E所成角的余弦值;
(2)求直线AC1与平面BED1F所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABCA1B1C1中,AB⊥AC,AB=2,AC=4,AA1=2,![]() =λ
=λ![]() .
.
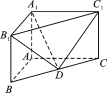
(1)若λ=1,求直线DB1与平面A1C1D所成角的正弦值;
(2)若二面角B1- A1C1-D的大小为60°,求实数λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌奶茶公司计划在A地开设若干个连锁加盟店,经调查研究,加盟店的个数x与平均每个店的月营业额y(万元)具有如下表所示的数据关系:
x | 2 | 4 | 6 | 8 | 10 |
y | 20.9 | 20.2 | 19 | 17.8 | 17.1 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的结果分析,为了保证平均每个加盟店的月营业额不少于14.6万元,则A地开设加盟店的个数不能超过几个?
参考公式:线性回归方程![]() 中的斜率和截距的最小二乘估计公式分别为
中的斜率和截距的最小二乘估计公式分别为
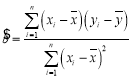 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
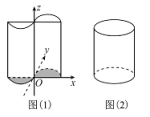
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图(1),函数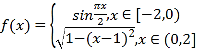 的图象与x轴围成一个封闭区域A(阴影部分),将区域A(阴影部分)沿z轴的正方向上移6个单位,得到一几何体.现有一个与之等高的底面为椭圆的柱体如图(2)所示,其底面积与区域A(阴影部分)的面积相等,则此柱体的体积为______.
的图象与x轴围成一个封闭区域A(阴影部分),将区域A(阴影部分)沿z轴的正方向上移6个单位,得到一几何体.现有一个与之等高的底面为椭圆的柱体如图(2)所示,其底面积与区域A(阴影部分)的面积相等,则此柱体的体积为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com