
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 的单调区间;
的单调区间;
(3)若函数![]() 在区间
在区间![]() 内有且只有一个极值点,求
内有且只有一个极值点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)见解析(Ⅲ)
(Ⅱ)见解析(Ⅲ)![]()
【解析】
(Ⅰ)根据导数的几何意义求出切线的斜率,由点斜式方程可得答案;(Ⅱ)对m进行讨论,解![]() 可得函数的增区间,解
可得函数的增区间,解![]() 得函数的减区间;(III)由题意可知g′(x)=0在(1,2)上有解,讨论m的范围,判断g′(x)的单调性和零点个数,得出结论.
得函数的减区间;(III)由题意可知g′(x)=0在(1,2)上有解,讨论m的范围,判断g′(x)的单调性和零点个数,得出结论.
(Ⅰ)当![]() 时,
时,![]() ,
,
所以![]() ,
,![]() .
.
又![]() ,
,
所以曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
(Ⅱ)函数![]() 的定义域为
的定义域为![]() .
.
![]() ,
,
(1)当![]() 即
即![]() 时,
时,
因为![]() ,
,![]() ,
,
所以![]() 的单调增区间为
的单调增区间为![]() ,无单调减区间.
,无单调减区间.
(2)当![]() ,即
,即![]() 时,令
时,令![]() ,得
,得![]()
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
所以![]() 的单调增区间为
的单调增区间为![]() ,减区间为
,减区间为![]() .
.
综上,当![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ,无单调减区间;
,无单调减区间;
当![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ,减区间为
,减区间为![]() .
.
(Ⅲ)因为![]() ,
,
所以![]() .
.
令![]() .
.
若函数![]() 在区间
在区间![]() 内有且只有一个极值点,
内有且只有一个极值点,
则函数![]() 在区间
在区间![]() 内存在零点.
内存在零点.
又![]() ,
,
所以![]() 在
在![]() 内有唯一零点
内有唯一零点![]() .
.
且![]() 时,
时,![]()
![]() 时,
时,![]()
则![]() 在
在![]() 内为减函数,在
内为减函数,在![]() 内为增函数.
内为增函数.
又因为![]() 且
且![]() 在
在![]() 内存在零点,
内存在零点,
所以![]()
解得![]() .
.
显然![]() 在
在![]() 内有唯一零点,记为
内有唯一零点,记为![]() .
.
当![]() 时,
时,![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 点两侧异号,即
点两侧异号,即![]() 在
在![]() 点两侧异号,
点两侧异号,![]() 为函数
为函数![]() 在区间
在区间![]() 内唯一极值点.
内唯一极值点.
当![]() 时,
时,![]()
又![]() 在
在![]() 内成立,
内成立,
所以![]() 在
在![]() 内单调递增,故
内单调递增,故![]() 无极值点.
无极值点.
当![]() 时,
时,![]() 易得
易得![]() 时,
时,![]() 故
故![]() 无极值点.
无极值点.
所以当且仅当![]() 时,函数
时,函数![]() 在区间
在区间![]() 内有且只有一个极值点.
内有且只有一个极值点.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】以下关于圆锥曲线的命题中:①双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点;②设
有相同的焦点;②设![]() 、
、![]() 是两个定点,
是两个定点,![]() 为非零常数,若
为非零常数,若![]() ,则动点
,则动点![]() 的轨迹为双曲线的一支;③设点
的轨迹为双曲线的一支;③设点![]() 、
、![]() 分别是定圆
分别是定圆![]() 上一个定点和动点,
上一个定点和动点,![]() 为坐标原点,若
为坐标原点,若![]() ,则动点
,则动点![]() 的轨迹为圆;其中真命题是_________.(写出所有真命题的序号)
的轨迹为圆;其中真命题是_________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 垂直于同一个平面的两条直线平行
B. 若两个平面垂直,则其中一个平面内垂直于这两个平面交线的直线与另一个平面垂直
C. 一个平面内的两条相交直线均与另一个平面平行,则这两个平面平行
D. 一条直线与一个平面内的无数条直线垂直,则这条直线和这个平面垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
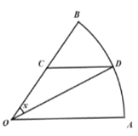
【题目】为庆祝某校一百周年校庆,展示该校一百年来的办学成果及优秀校友风采,学校准备校庆期间搭建一个扇形展览区,如图,是一个半径为2百米,圆心角为![]() 的扇形展示区的平面示意图.点
的扇形展示区的平面示意图.点![]() 是半径
是半径![]() 上一点,点
上一点,点![]() 是圆弧
是圆弧![]() 上一点,且
上一点,且![]() .为了实现“以展养展”,现决定:在线段
.为了实现“以展养展”,现决定:在线段![]() 、线段
、线段![]() 及圆弧
及圆弧![]() 三段所示位置设立广告位,经测算广告位出租收入是:线段
三段所示位置设立广告位,经测算广告位出租收入是:线段![]() 处每百米为
处每百米为![]() 元,线段
元,线段![]() 及圆弧
及圆弧![]() 处每百米均为
处每百米均为![]() 元.设
元.设![]() 弧度,广告位出租的总收入为
弧度,广告位出租的总收入为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)试问![]() 为何值时,广告位出租的总收入最大,并求出其最大值.
为何值时,广告位出租的总收入最大,并求出其最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)一种画椭圆的工具如图1所示.![]() 是滑槽
是滑槽![]() 的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且
的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且![]() ,
,![]() .当栓子D在滑槽AB内作往复运动时,带动N绕
.当栓子D在滑槽AB内作往复运动时,带动N绕![]() 转动,M处的笔尖画出的椭圆记为C.以
转动,M处的笔尖画出的椭圆记为C.以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴建立如图2所示的平面直角坐标系.
轴建立如图2所示的平面直角坐标系.
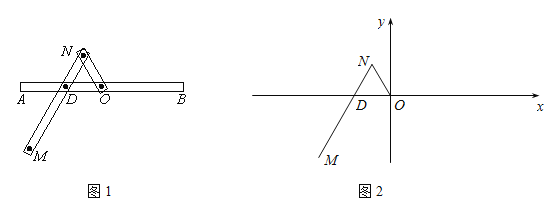
(Ⅰ)求椭圆C的方程;
(Ⅱ)设动直线![]() 与两定直线
与两定直线![]() 和
和![]() 分别交于
分别交于![]() 两点.若直线
两点.若直线![]() 总与椭圆
总与椭圆![]() 有且只有一个公共点,试探究:
有且只有一个公共点,试探究:![]() 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
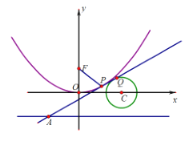
【题目】已知如图,直线![]() 是抛物线
是抛物线![]() (
(![]() )和圆C:
)和圆C:![]() 的公切线,切点(在第一象限)分别为P、Q.F为抛物线的焦点,切线
的公切线,切点(在第一象限)分别为P、Q.F为抛物线的焦点,切线![]() 交抛物线的准线于A,且
交抛物线的准线于A,且![]() .
.
(1)求切线![]() 的方程;
的方程;
(2)求抛物线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,椭圆的离心率为
,椭圆的离心率为![]() ,过椭圆
,过椭圆![]() 的左焦点
的左焦点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() ,与以右焦点
,与以右焦点![]() 为圆心,半径为
为圆心,半径为![]() 的圆
的圆![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)线段![]() 是椭圆
是椭圆![]() 过右焦点
过右焦点![]() 的弦,且
的弦,且![]() ,求
,求![]() 的面积的最大值以及取最大值时实数
的面积的最大值以及取最大值时实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商家耗资4500万元购进一批![]() (虚拟现实)设备,经调试后计划明年开始投入使用,由于设备损耗和维护,第一年需维修保养费用200万元,从第二年开始,每年的维修保并费用比上一年增40万元.该设备使用后,每年的总收入为2800万元.
(虚拟现实)设备,经调试后计划明年开始投入使用,由于设备损耗和维护,第一年需维修保养费用200万元,从第二年开始,每年的维修保并费用比上一年增40万元.该设备使用后,每年的总收入为2800万元.
(1)求盈利额![]() (万元)与使用年数
(万元)与使用年数![]() 之间的函数关系式;
之间的函数关系式;
(2)该设备使用多少年,商家的年平均盈利额最大?最大年平均盈利额是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com