Question

14．某连锁经营公司所属5个零售店某月的销售额和利润额资料如表：

商店名称	A	B	C	D	E
销售额x/千万元	3	5	6	7	9
利润额y/百万元	2	3	3	4	5

（1）画出销售额和利润额的散点图；
（2）若销售额和利润额具有相关关系，用最小二乘法计算利润额y对销售额x的回归直线方程；
（3）据（2）的结果估计当销售额为1亿元时的利润额．

Answer 1

分析 （1）根据某连锁经营公司所属5个零售店某月的销售额和利润额的表中数据画出散点图，根据这些点分布在某直线附近判断是否具有相关关系；
（2）求出线性回归系数，可得利润额y对销售额x的回归直线方程；
（3）将零售店某月销售额为10千万元代入线性回归方程，计算出y的值，即为此月份该零售点的估计值．

解答 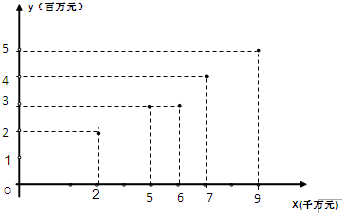解：（1）销售额与利润额成线性相关关系；
（2）由已知数据计算得：$\overline{x}$=6，$\overline{y}$=3.4，
b=$\frac{112-5×6×3.4}{200-6×6×6}$=0.5，
a=3.4-0.5×6=0.4
∴y对销售额x的回归直线方程为：
y=0.5x+0.4；
（3）∴当销售额为1亿元时，
将x=10代入线性回归方程中得到y=5.4（千万元）．

点评 本题考查线性回归方程，解题的关键是掌握住线性回归方程中系数的求法公式及线性回归方程的形式，按公式中的计算方法求得相关的系数，得出线性回归方程．