
| A. | (1,$\frac{2}{3}$) | B. | (1,$\frac{1}{3}$) | C. | ($\frac{1}{3}$,1) | D. | ($\frac{2}{3}$,1) |
分析 根据抛物线的方程求出准线方程,利用抛物线的定义抛物线上的点到焦点的距离等于到准线的距离,列出方程求出A,B的中点横坐标的和,可得线段AB的中点横坐标,利用点差法,结合直线AB的斜率为3,可得线段AB的中点纵坐标,即可求出线段AB的中点P的坐标.
解答 解:∵F是抛物线y2=2x的焦点,
∴F($\frac{1}{2}$,0),准线方程x=-$\frac{1}{2}$.
设A(x1,y1),B(x2,y2)
∴|AF|+|BF|=x1+$\frac{1}{2}$+x2+$\frac{1}{2}$=3,
∴x1+x2=2,
∴线段AB的中点横坐标为1,
∵y2=2x,
∴y12=2x1,y22=2x2,
∴(y1+y2)(y1-y2)=2(x1-x2)
∵直线AB的斜率为3,
∴y1+y2=$\frac{2}{3}$
∴线段AB的中点纵坐标为$\frac{1}{3}$.
故选:B.
点评 本题考查解决抛物线上的点到焦点的距离问题,解题的关键是利用抛物线的定义将到焦点的距离转化为到准线的距离.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1+$\sqrt{6}$ | B. | -1+2$\sqrt{6}$ | C. | -1+$\sqrt{5}$ | D. | -1+2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(0)<f(-$\frac{1}{3}$)<f($\frac{2}{5}$) | B. | f(-$\frac{1}{3}$)<f(0)<f($\frac{2}{5}$) | C. | f($\frac{2}{5}$)<f(-$\frac{1}{3}$)<f(0) | D. | f(0)<f($\frac{2}{5}$)<f(-$\frac{1}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
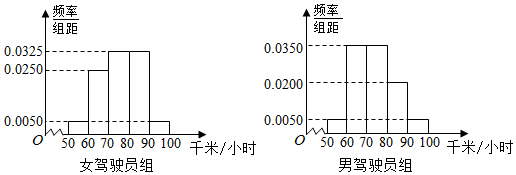
| 危险驾驶 | 非危险驾驶 | 合计 | |
| 男驾驶员 | 15 | 45 | 60 |
| 女驾驶员 | 15 | 25 | 40 |
| 合计 | 30 | 70 | 100 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 正方体ABCD-A1B1C1D1中,点M是CD的中点.
正方体ABCD-A1B1C1D1中,点M是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com