
分析 根据已知中的等式,分析等式两边式子的变化规律,可得答案.
解答 解:由已知中的等式:
$\frac{1+(\frac{1}{2})^{2}}{1+{2}^{2}}$=($\frac{1+\frac{1}{2}}{1+2}$)2,
$\frac{1+{4}^{3}}{1+(\frac{1}{4})^{3}}$=($\frac{1+4}{1+\frac{1}{4}}$)3,
$\frac{{1+{{({-\frac{{\sqrt{2}}}{2}})}^4}}}{{1+{{({-\sqrt{2}})}^4}}}={({\frac{{1-\frac{{\sqrt{2}}}{2}}}{{1-\sqrt{2}}}})^4}$,
…,
归纳可得:等式左边的分子为1+an,分母为1+bn,
等式右边的底数为:$\frac{1+a}{1+b}$,指数为n,
故得到的一般规律为:$\frac{1+{a}^{n}}{1+{b}^{n}}=(\frac{1+a}{1+b})^{n}$,
故答案为:$\frac{1+{a}^{n}}{1+{b}^{n}}=(\frac{1+a}{1+b})^{n}$
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{2}{3}$) | B. | (1,$\frac{1}{3}$) | C. | ($\frac{1}{3}$,1) | D. | ($\frac{2}{3}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
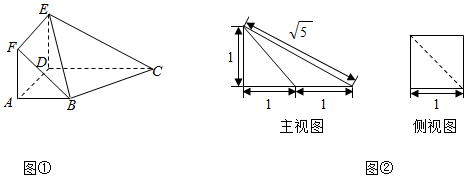 如图,图②为图①空间图形的主视图和侧视图,其中侧视图为正方形.在图①中,设平面BEF与平面ABCD相交于直线l.
如图,图②为图①空间图形的主视图和侧视图,其中侧视图为正方形.在图①中,设平面BEF与平面ABCD相交于直线l.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{e}$,1) | B. | (0,$\frac{1}{e}$)∪(1,+∞) | C. | ($\frac{1}{e}$,e) | D. | (0,1)∪(e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 3:1 | B. | 1:3 | C. | 4:1 | D. | 3:2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com