练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近于圆的面积，并创立了“割圆术”，利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”．如图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出的（四舍五入精确到小数点后两位）的值为（ ）（参考数据：sin15°=0.2588，sin75°=0.1305）
    A.3.10
    B.3.11
    C.3.12
    D.3.13

    【答案】B
    【解析】解：模拟执行程序，可得： k=0，S=3sin60°= ，
    k=1，S=6×sin30°=3，
    k=2，S=12×sin15°=12×0.2588=3.1056≈3.11，
    退出循环，输出的值为3.11．
    故选：B．
    列出循环过程中S与k的数值，满足判断框的条件即可结束循环．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知幂函数为偶函数.

    （1）求的解析式；

    （2）若函数在区间(2,3)上为单调函数，求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某快递公司在某市的货物转运中心，拟引进智能机器人分拣系统，以提高分拣效率和降低物流成本，已知购买x台机器人的总成本p(x)＝万元．

    (1)若使每台机器人的平均成本最低，问应买多少台？

    (2)现按(1)中的数量购买机器人，需要安排m人将邮件放在机器人上，机器人将邮件送达指定落袋格口完成分拣，经实验知，每台机器人的日平均分拣量q(m)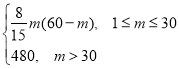＝ (单位：件)，已知传统人工分拣每人每日的平均分拣量为1200件，问引进机器人后，日平均分拣量达最大值时，用人数量比引进机器人前的用人数量最多可减少百分之几？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图半圆柱OO1的底面半径和高都是1，面ABB1A1是它的轴截面（过上下底面圆心连线OO1的平面），Q，P分别是上下底面半圆周上一点．
    （1）证明：三棱锥Q﹣ABP体积VQ﹣ABP≤ ，并指出P和Q满足什么条件时有AP⊥BQ
    （2）求二面角P﹣AB﹣Q平面角的取值范围，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中为实数.

    （1）若曲线在点处的切线方程为，试求函数的单调区间；

    （2）当，，且时，若恒有，试求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在多面体ABCDEF中，底面ABCD为正方形，平面AED⊥平面ABCD，AB= EA= ED，EF∥BD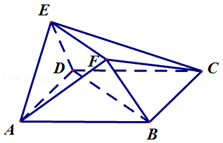
    （I）证明：AE⊥CD
    （II）在棱ED上是否存在点M，使得直线AM与平面EFBD所成角的正弦值为 ？若存在，确定点M的位置；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f(x)＝(m2－m－1)·是幂函数，对任意x1，x2∈(0，＋∞)且x1≠x2，满足，若a，b∈R且a＋b>0，ab<0，则f(a)＋f(b)的值(　　)

    A. 恒大于0 B. 恒小于0

    C. 等于0 D. 无法判断

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C：y2=2px（p＞0）上的点M（x0 ， y0）到点N（2，0）距离的最小值为 ．
    （1）求抛物线C的方程；
    （2）若x0＞2，圆E（x﹣1）2+y2=1，过M作圆E的两条切线分别交y轴A（0，a），B（0，b）两点，求△MAB面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中xOy，直线C1的参数方程为 （t是参数）．在以坐标原点为极点，x轴非负半轴为极轴的极坐标系中，曲线C2的极坐标方程为ρ=sinθ﹣cosθ（θ是参数）．
    （Ⅰ）将曲线C2的极坐标方程化为直角坐标方程，并判断曲线C2所表示的曲线；
    （Ⅱ）若M为曲线C2上的一个动点，求点M到直线C1的距离的最大值和最小值．

    查看答案和解析>>

    同步练习册答案