
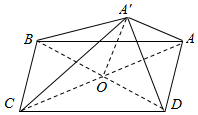
 平行四边形ABCD中,AB=$\sqrt{13}$,BC=$\sqrt{5}$,BD=4,AC,BD交于O,将△ABD沿BD折起至△A′BD,使得A′C⊥CB.
平行四边形ABCD中,AB=$\sqrt{13}$,BC=$\sqrt{5}$,BD=4,AC,BD交于O,将△ABD沿BD折起至△A′BD,使得A′C⊥CB.分析 (1)根据线面垂直的判定定理即可证明A′C⊥平面A′AD;
(2)过C作CE⊥BD于E,过A作AF⊥BD于F,则$\overrightarrow{EC}$与$\overrightarrow{FA′}$所成的角即为二面角A′-BD-C所成的角,利用向量的数量积的公式进行求解即可求二面角A′-BD-C的余弦值.
解答 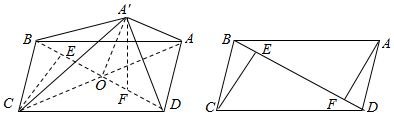 证明:(1)∵A′C⊥CB,CB∥AD,
证明:(1)∵A′C⊥CB,CB∥AD,
∴A′C⊥AD,
∵AB=$\sqrt{13}$,BC=$\sqrt{5}$,
∴A′B=$\sqrt{13}$,BC=$\sqrt{5}$,
则A′C=$\sqrt{A′{B}^{2}-B{C}^{2}}$=$\sqrt{13-5}=\sqrt{8}$=2$\sqrt{2}$,
∵A′D=AD=BC=$\sqrt{5}$,
∴A′C2+A′D2=($\sqrt{8}$)+($\sqrt{5}$)2=13=CD2,
则△A′CD为直角三角形,
则A′C⊥A′D,
∵A′D∩AD=D,
∴A′C⊥平面A′AD;
(2)过C作CE⊥BD于E,过A作AF⊥BD于F,
∵AB=$\sqrt{13}$,BC=$\sqrt{5}$,BD=4,
∴cos∠BDC=$\frac{C{D}^{2}+B{D}^{2}-B{C}^{2}}{2CD•BD}$=$\frac{13+16-5}{2\sqrt{13}×4}=\frac{24}{8\sqrt{13}}$=$\frac{3}{\sqrt{13}}$,
则sin∠BDC=$\sqrt{1-(\frac{3}{\sqrt{13}})^{2}}$=$\sqrt{1-\frac{9}{13}}$=$\frac{2}{\sqrt{13}}$,
∵sin∠BDC=$\frac{CE}{CD}$=$\frac{CE}{\sqrt{13}}$=$\frac{2}{\sqrt{13}}$,
即CE=2.同理AF=CE=2,
DE=CDcos∠BDC=$\sqrt{13}$×$\frac{3}{\sqrt{13}}$=3,
则BE=BD-DE=4-3=1,
则BE=DF=1,EF=3-1=2,
则$\overrightarrow{EC}$与$\overrightarrow{FA′}$所成的角即为二面角A′-BD-C所成的角,
∵$\overrightarrow{A′C}$=$\overrightarrow{CE}$+$\overrightarrow{EF}$+$\overrightarrow{FA′}$,
∴平方得$\overrightarrow{A′C}$=$\overrightarrow{CE}$+$\overrightarrow{EF}$+$\overrightarrow{FA′}$,
$\overrightarrow{A′C}$2=($\overrightarrow{CE}$+$\overrightarrow{EF}$+$\overrightarrow{FA′}$ )2=$\overrightarrow{CE}$2+$\overrightarrow{EF}$2+$\overrightarrow{FA′}$ 2+$\overrightarrow{CE}$•$\overrightarrow{EF}$+$\overrightarrow{FA′}$•$\overrightarrow{CE}$+$\overrightarrow{EF}$•$\overrightarrow{FA′}$,
即8=4+4+4-2×2×2cos<$\overrightarrow{EC}$,$\overrightarrow{FA′}$>,
即8cos<$\overrightarrow{EC}$,$\overrightarrow{FA′}$>=4,
则cos<$\overrightarrow{EC}$,$\overrightarrow{FA′}$>=$\frac{1}{2}$,
则二面角A′-BD-C的余弦值是$\frac{1}{2}$.
点评 本题主要考查线面垂直的判定以及二面角的求解,利用向量的应用,结合向量的数量积的应用是解决本题的关键.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:选择题
| A. | ?x0∈(0,$\frac{π}{2}$),cosx0≤sinx0 | B. | ?x∈(0,$\frac{π}{2}$),cosx≤sinx | ||
| C. | ?x∈(0,$\frac{π}{2}$),cosx>sinx | D. | ?x0∉(0,$\frac{π}{2}$),cosx0>sinx0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
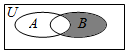 若全集U=R,A={0,1,2,3},B={2,3,4,5},则Venn图中阴影部分表示的集合为( )
若全集U=R,A={0,1,2,3},B={2,3,4,5},则Venn图中阴影部分表示的集合为( )| A. | {0,1} | B. | {2,3} | C. | {4,5} | D. | {0,1,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com