
分析 (1)根据x=ρcosθ、y=ρsinθ可得点P的直角坐标;
(2)利用参数的几何意义,即可求|PA|•|PB|.
解答 解:(1)点P的极坐标为(1,$\frac{π}{2}$),直角坐标为(0,1)
(2)倾斜角等于$\frac{2π}{3}$的直线l经过P,参数方程为$\left\{\begin{array}{l}{x=-\frac{1}{2}t}\\{y=1+\frac{\sqrt{3}}{2}t}\end{array}\right.$,
曲线C的参数方程为$\left\{\begin{array}{l}{x=2t}\\{y=16{t}^{2}-9}\end{array}\right.$,普通方程为y=4x2-9,
代入可得t2-$\frac{\sqrt{3}}{2}$t-10=0,
∵点P的坐标为(0,1),
∴|PA|•|PB|=-10.
点评 本小题主要考查参数方程、极坐标方程等基础知识,考查参数的几何意义,考查运算求解能力,属于中档题.


科目:高中数学 来源: 题型:解答题
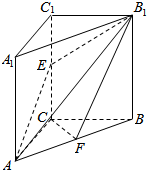 已知在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=1,BC=2,AA1=4.当E为CC1中点时,
已知在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=1,BC=2,AA1=4.当E为CC1中点时,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),点(-1,$\frac{\sqrt{2}}{2}$)在椭圆C上,点T满足$\overrightarrow{OT}$=$\frac{{a}^{2}}{\sqrt{{a}^{2}-{b}^{2}}}$•$\overrightarrow{OF}$(其中O为坐标原点),过点F作一斜率为1的直线交椭圆于P、Q两点(其中P点在x轴上方,Q点在x轴下方)
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),点(-1,$\frac{\sqrt{2}}{2}$)在椭圆C上,点T满足$\overrightarrow{OT}$=$\frac{{a}^{2}}{\sqrt{{a}^{2}-{b}^{2}}}$•$\overrightarrow{OF}$(其中O为坐标原点),过点F作一斜率为1的直线交椭圆于P、Q两点(其中P点在x轴上方,Q点在x轴下方)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y+5=0 | B. | 2x+y-5=0 | C. | 2x-y+5=0(2≤x≤3) | D. | 2x+y-5=0(2≤x≤3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组数 | 分组 | 频数 | 频率 | “光盘族”占本组比例 |
| 第1组 | [25,30) | 50 | 0.05 | 30% |
| 第2组 | [30,35) | 100 | 0.10 | 30% |
| 第3组 | [35,40) | 150 | 0.15 | 40% |
| 第4组 | [40,45) | 200 | 0.20 | 50% |
| 第5组 | [45,50) | a | b | 65% |
| 第6组 | [50,55) | 200 | 0.20 | 60% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com