
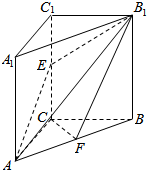
 已知在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=1,BC=2,AA1=4.当E为CC1中点时,
已知在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=1,BC=2,AA1=4.当E为CC1中点时,分析 (1)可分别以CA,CB,CC1三直线为x,y,z轴,建立空间直角坐标系,根据已知的边的长度,求出所有点的坐标即可;
(2)求出向量$\overrightarrow{AE},\overrightarrow{CF}$的坐标,然后求出$cos<\overrightarrow{AE},\overrightarrow{CF}>$,从而得出异面直线AE与CF所成角的余弦值;
(3)先求出$\overrightarrow{C{B}_{1}}$的坐标,可设平面CFB1的法向量为$\overrightarrow{m}$,根据$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{CF}=0}\\{\overrightarrow{m}•\overrightarrow{C{B}_{1}}=0}\end{array}\right.$即可得出法向量$\overrightarrow{m}$,同样的方法可求出平面AB1E的坐标.
解答 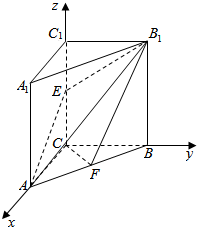 解:(1)根据条件知,CA,CB,CC1三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,则可确定各点坐标:
解:(1)根据条件知,CA,CB,CC1三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,则可确定各点坐标:
C(0,0,0),A(1,0,0),B(0,2,0),F($\frac{1}{2},1,0$),A1(1,0,4),B1(0,2,4),C1(0,0,4),E(0,0,2);
(2)$\overrightarrow{AE}=(-1,0,2),\overrightarrow{CF}=(\frac{1}{2},1,0)$;
∴$cos<\overrightarrow{AE},\overrightarrow{CF}>=\frac{\overrightarrow{AE}•\overrightarrow{CF}}{|\overrightarrow{AE}||\overrightarrow{CF}|}$=$\frac{-\frac{1}{2}}{\sqrt{5}•\frac{\sqrt{5}}{2}}=-\frac{1}{5}$;
∴异面直线AE与CF所成角的余弦值为$\frac{1}{5}$;
(3)$\overrightarrow{C{B}_{1}}=(0,2,4)$;
设平面CFB1的法向量为$\overrightarrow{m}=({x}_{1},{y}_{1},{z}_{1})$,则:
$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{CF}=\frac{1}{2}{x}_{1}+{y}_{1}=0}\\{\overrightarrow{m}•\overrightarrow{C{B}_{1}}=2{y}_{1}+4{z}_{1}=0}\end{array}\right.$;
取y1=2,则x1=-4,z1=-1,∴$\overrightarrow{m}=(-4,2,-1)$;
即平面CFB1的法向量为(-4,2,-1);
同理,设平面AB1E的法向量为$\overrightarrow{n}=({x}_{2},{y}_{2},{z}_{2})$,$\overrightarrow{A{B}_{1}}=(-1,2,4)$,$\overrightarrow{AE}=(-1,0,2)$,则:
$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{A{B}_{1}}=-{x}_{2}+2{y}_{2}+4{z}_{2}=0}\\{\overrightarrow{n}•\overrightarrow{AE}=-{x}_{2}+2{z}_{2}=0}\end{array}\right.$;
取z2=1,则$\overrightarrow{n}=(2,-1,1)$;
即平面AB1E的法向量为(2,-1,1).
点评 考查建立空间直角坐标系,利用空间向量求异面直线所成角,及平面法向量的方法,线面垂直的概念,向量夹角余弦的坐标公式,要弄清异面直线所成角和异面直线的方向向量夹角的关系,以及平面法向量的概念及求法.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 视α的大小而定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ab≤$\frac{1}{8}$ | B. | ab≥$\frac{1}{8}$ | C. | ab$≥\frac{1}{4}$ | D. | ab$≤\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
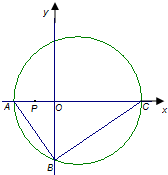 如图,直角三角形ABC的顶点坐标A(-2,0),直角顶点$B(0,-2\sqrt{2})$,顶点C在x轴上,点P为线段OA的中点.
如图,直角三角形ABC的顶点坐标A(-2,0),直角顶点$B(0,-2\sqrt{2})$,顶点C在x轴上,点P为线段OA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com