
【题目】已知![]() ,
, ![]() 是
是![]() 的导函数.
的导函数.
(Ⅰ)求![]() 的极值;
的极值;
(Ⅱ)若![]() 在
在![]() 时恒成立,求实数
时恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)当![]() 时,有极小值
时,有极小值![]() ,无极大值;(Ⅱ)
,无极大值;(Ⅱ) ![]()
【解析】试题分析:
(Ⅰ)结合导函数分类讨论可得当![]() 时,
时, ![]() 无极值;当
无极值;当![]() ,
, ![]() 时,有极小值
时,有极小值![]() .
.
(Ⅱ)结合题意构造新函数![]() ,结合函数的性质可得实数
,结合函数的性质可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(Ⅰ)![]() ,
, ![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 无极值;
无极值;
当![]() 时,
时, ![]() ,解得
,解得![]() ,
,
由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ,
,
所以当![]() 时,有极小值
时,有极小值![]() .
.
(Ⅱ)令![]() ,则
,则![]() ,注意到
,注意到![]() ,
,
解法一: ![]() ,
,
①当![]() 时,由
时,由![]() ,得
,得![]() ,即
,即![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 时,
时, ![]() ,从而
,从而![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 时,
时, ![]() ,即
,即![]() 恒成立.
恒成立.
②当![]() 时,由
时,由![]() 解得
解得![]() ,即
,即![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() 时,
时, ![]() ,从而
,从而![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() 时,
时, ![]() ,即
,即![]() 不成立.
不成立.
综上, ![]() 的取值范围为
的取值范围为![]() .
.
解法二:令![]() ,则
,则![]() ,由
,由![]() ,得
,得![]() ;
; ![]() ,得
,得![]() ,
,
∴![]() ,即
,即![]() 恒成立,
恒成立,
故![]() ,
,
当![]() 时,
时, ![]() ,于是
,于是![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() 成立.
成立.
当![]() 时,由
时,由![]() 可得
可得![]() .
.
![]()
![]() ,
,
故当![]() 时,
时, ![]() ,
,
于是当![]() 时,
时, ![]() 单调递减,
单调递减, ![]() ,
, ![]() 不成立.
不成立.
综上, ![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD是正方形,分E,F,G别为PD,AB,CD的中点,PD⊥平面ABCD 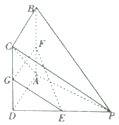
(1)证明AC⊥PB
(2)证明:平面PBC∥平面EFG.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们称满足: ![]() (
(![]() )的数列
)的数列![]() 为“
为“![]() 级梦数列”.
级梦数列”.
(1)若![]() 是“
是“![]() 级梦数列”且
级梦数列”且![]() .求:
.求: ![]() 和
和![]() 的值;
的值;
(2)若![]() 是“
是“![]() 级梦数列”且满足
级梦数列”且满足![]() ,
, ![]() ,求
,求![]() 的最小值;
的最小值;
(3)若![]() 是“0级梦数列”且
是“0级梦数列”且![]() ,设数列
,设数列![]() 的前
的前![]() 项和为
项和为![]() .证明:
.证明: ![]() (
(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a|log2x|+1(a≠0),定义函数F(x)= ![]() ,给出下列命题:
,给出下列命题:
①F(x)=|f(x)|;
②函数F(x)是偶函数;
③当a<0时,若0<m<n<1,则有F(m)﹣F(n)<0成立;
④当a>0时,函数y=F(x)﹣2有4个零点.
其中正确命题的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() :
:  (
(![]() 为参数),在以
为参数),在以![]() 原点为极点,
原点为极点, ![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() ,
, ![]() 两点,求点
两点,求点![]() 到
到![]() ,
, ![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是一个非空集合,
是一个非空集合, ![]() 是定义在
是定义在![]() 上的一个运算.如果同时满足下述四个条件:
上的一个运算.如果同时满足下述四个条件:
(1)对于![]() ,都有
,都有![]() ;
;
(2)对于![]() ,都有
,都有![]() ;
;
(3)对于![]() ,使得
,使得![]() ;
;
(4)对于![]() ,使得
,使得![]() (注:“
(注:“![]() ”同(iii)中的“
”同(iii)中的“![]() ”).
”).
则称![]() 关于运算
关于运算![]() 构成一个群.现给出下列集合和运算:
构成一个群.现给出下列集合和运算:
①![]() 是整数集合,
是整数集合, ![]() 为加法;②
为加法;②![]() 是奇数集合,
是奇数集合, ![]() 为乘法;③
为乘法;③![]() 是平面向量集合,
是平面向量集合, ![]() 为数量积运算;④
为数量积运算;④![]() 是非零复数集合,
是非零复数集合, ![]() 为乘法. 其中
为乘法. 其中![]() 关于运算
关于运算![]() 构成群的序号是___________(将你认为正确的序号都写上).
构成群的序号是___________(将你认为正确的序号都写上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前n项和为
的前n项和为![]() ,
, ![]() ,
, ![]() ,数列
,数列![]() 满足:
满足: ![]() ,
, ![]() ,
, ![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]()
(1)求数列![]() 的通项公式及前n项和;
的通项公式及前n项和;
(2)求数列![]() 的通项公式及前n项和;
的通项公式及前n项和;
(3)记集合 ,若M的子集个数为16,求实数
,若M的子集个数为16,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com