
分析 (1)当a=2时,f(x)=-x(x-2)=-(x-1)2+1.即可得出函数f(x)的单调区间.
(2)函数$y=-{(x-\frac{a}{2})^2}+\frac{a^2}{4}$图象开口向下,对称轴方程为$x=\frac{a}{2}$,对$\frac{a}{2}$与区间端点±1的大小关系分类讨论即并且结合图象可得出.
解答 解:(1)当a=2时,f(x)=-x(x-2)=-(x-1)2+1.
∴函数f(x)的单调增区间(-∞,1],单调减区间[1,+∞).
(2)函数$y=-{(x-\frac{a}{2})^2}+\frac{a^2}{4}$图象开口向下,对称轴方程为$x=\frac{a}{2}$,
1:当$\frac{a}{2}<-1$,即a<-2时,由图可知,当x=-1时,ymax=-a-1;
2:当$-1≤\frac{a}{2}≤1$,即-2≤a≤2时,由图可知,当$x=\frac{a}{2}$时,${y_{max}}=\frac{a^2}{4}$;
3:当$\frac{a}{2}>1$,即a>2时,由图可知,当x=1时,ymax=a-1;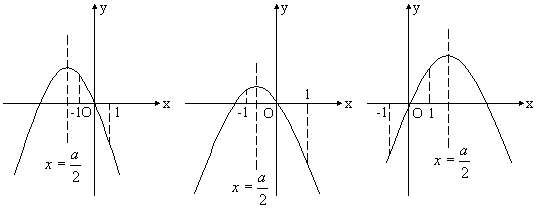
故${y_{max}}=\left\{\begin{array}{l}-(a+1)\;,\;a<-2\\ \frac{a^2}{4}\;,\;-2≤a≤2\\ a-1\;,\;a>2\end{array}\right.$.
点评 本题考查了二次函数的图象与性质、分类讨论方法,考查了推理能力与计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
 随着智能手机的普及,网络购物越来越受到人们的青睐,某研究性学习小组对使用智能手机的利与弊随机调查了10位同学,得到的满意度打分如茎叶图所示.若这组数据的中位数、平均数分别为a,b,则a,b的大小关系是a=b.
随着智能手机的普及,网络购物越来越受到人们的青睐,某研究性学习小组对使用智能手机的利与弊随机调查了10位同学,得到的满意度打分如茎叶图所示.若这组数据的中位数、平均数分别为a,b,则a,b的大小关系是a=b.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{7}$ | B. | $\frac{7}{3}$ | C. | $\frac{7}{12}$ | D. | $\frac{12}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{2}$ | B. | -π-1 | C. | -π+1 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com