
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 且侧棱
且侧棱![]() 其中
其中![]() 为
为![]() 的
的![]() 交点.
交点.

(1)求点![]() 到平面
到平面![]() 的距离;
的距离;
(2)在线段![]() 上,是否存在一个点
上,是否存在一个点![]() ,使得直线
,使得直线![]() 与
与![]() 垂直?若存在,求出线段
垂直?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则称
,则称![]() 是“
是“![]() 数列”.
数列”.
(1)若![]() 是“
是“![]() 数列”,且
数列”,且![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() 是等差数列,首项为
是等差数列,首项为![]() ,公差为
,公差为![]() ,且
,且![]() ,判断
,判断![]() 是否为“
是否为“![]() 数列”;
数列”;
(3)设数列![]() 是等比数列,公比为
是等比数列,公比为![]() ,若数列
,若数列![]() 与
与![]() 都是“
都是“![]() 数列”,求
数列”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax,a∈R.
(1)若f(x)有两个零点,求a的取值范围;
(2)设函数g(x)![]() ,证明:g(x)有极大值,且极大值小于
,证明:g(x)有极大值,且极大值小于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某居民最近连续几年的月用水量进行统计,得到该居民月用水量![]() (单位:吨)的频率分布直方图,如图一.
(单位:吨)的频率分布直方图,如图一.
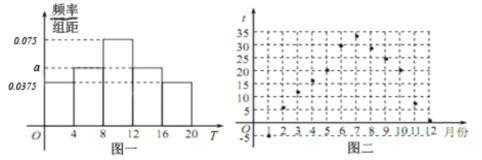
(1)求![]() 的值,并根据频率分布直方图估计该居民月平均用水量
的值,并根据频率分布直方图估计该居民月平均用水量![]() ;
;
(2)已知该居民月用水量![]() 与月平均气温
与月平均气温![]() (单位:℃)的关系可用回归直线
(单位:℃)的关系可用回归直线![]() 模拟.2019年当地月平均气温
模拟.2019年当地月平均气温![]() 统计图如图二,把2019年该居民月用水量高于和低于
统计图如图二,把2019年该居民月用水量高于和低于![]() 的月份作为两层,用分层抽样的方法选取5个月,再从这5个月中随机抽取2个月,求这2个月中该居民恰有1个月用水量超过
的月份作为两层,用分层抽样的方法选取5个月,再从这5个月中随机抽取2个月,求这2个月中该居民恰有1个月用水量超过![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆![]()
![]() 的离心率为
的离心率为![]() ,右准线的方程为
,右准线的方程为![]()
![]()
![]() 分别为椭圆C的左、右焦点,A,B分别为椭圆C的左、右顶点.
分别为椭圆C的左、右焦点,A,B分别为椭圆C的左、右顶点.
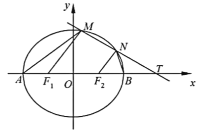
(1)求椭圆C的标准方程;
(2)过![]()
![]() 作斜率为
作斜率为![]()
![]() 的直线l交椭圆C于M,N两点(点M在点N的左侧),且
的直线l交椭圆C于M,N两点(点M在点N的左侧),且![]() ,设直线AM,BN的斜率分别为
,设直线AM,BN的斜率分别为![]()
![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )的周期为
)的周期为![]() ,图象的一个对称中心为
,图象的一个对称中心为![]() ,将函数
,将函数![]() 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得到的图象向右平移
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得到的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)求证:存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() 能按照某种顺序成等差数列.
能按照某种顺序成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,点P为双曲线C右支上异于顶点的一点,
,点P为双曲线C右支上异于顶点的一点,![]() 的内切圆与x轴切于点
的内切圆与x轴切于点![]() ,则a的值为______,若直线
,则a的值为______,若直线![]() 经过线段
经过线段![]() 的中点且垂直于线段
的中点且垂直于线段![]() ,则双曲线C的方程为________________.
,则双曲线C的方程为________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com