
(本小题满分10分)选修4-4:极坐标于参数方程
已知曲线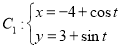 (
(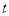 为参数),
为参数),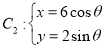 (
(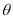 为参数).
为参数).
(1)化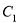 ,
, 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若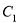 上的点
上的点 对应的参数为
对应的参数为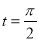 ,
,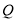 为
为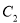 上的动点,求
上的动点,求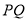 中点
中点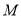 到直线
到直线 (
(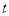 为参数)距离的最小值.
为参数)距离的最小值.
(1)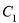 :
: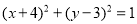 ,
,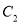 :
: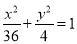 ,∴
,∴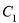 为圆心是
为圆心是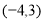 ,半径是
,半径是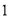 的圆,
的圆,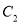 为中心是坐标原点,焦点在
为中心是坐标原点,焦点在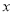 轴上,长半轴长是
轴上,长半轴长是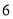 ,短半轴长是
,短半轴长是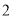 的椭圆;
的椭圆;
(2)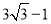 .
.
【解析】
试题分析:(1)分别消去两曲线参数方程中的参数得到两曲线的普通方程,即可得到曲线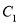 表示一个圆,曲线
表示一个圆,曲线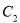 表示一个椭圆;
表示一个椭圆;
(2)把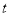 的值代入曲线
的值代入曲线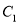 的参数方程得点
的参数方程得点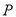 的坐标,然后把直线的参数方程化为普通方程,根据曲线
的坐标,然后把直线的参数方程化为普通方程,根据曲线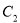 的参数方程设出
的参数方程设出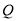 的坐标,利用中点坐标公式表示出点
的坐标,利用中点坐标公式表示出点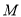 到已知直线的距离,利用辅助角化简后,利用正弦函数的值域即可得到距离的最小值.
到已知直线的距离,利用辅助角化简后,利用正弦函数的值域即可得到距离的最小值.
试题解析:(1)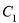 :
: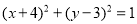 ,
,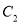 :
: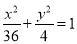 ,∴
,∴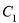 为圆心是
为圆心是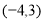 ,半径是
,半径是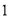 的圆,
的圆,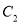 为中心是坐标原点,焦点在
为中心是坐标原点,焦点在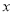 轴上,长半轴长是
轴上,长半轴长是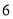 ,短半轴长是
,短半轴长是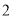 的椭圆;
的椭圆;
(2)当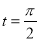 时,
时,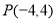 ,
,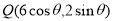 ,故
,故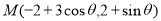 ,
,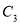 为直线
为直线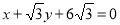 ,
,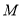 到
到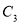 的距离
的距离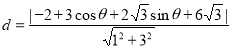
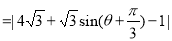 ,从而当
,从而当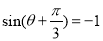 时,
时,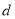 取得最小值
取得最小值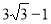 .
.
考点: 1.圆的参数方程,直线的参数方程;2.点到直线的距离公式;3.三角恒等变形.
考点分析: 考点1:参数方程 试题属性

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知三棱锥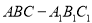 中,侧棱垂直于底面,点
中,侧棱垂直于底面,点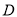 是
是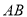 的中点.
的中点.
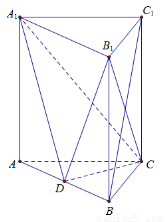
(1)求证: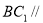 平面
平面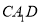 ;
;
(2)若底面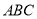 为边长为
为边长为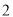 的正三角形,
的正三角形,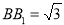 ,求三棱锥
,求三棱锥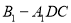 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试文科数学试卷(解析版) 题型:选择题
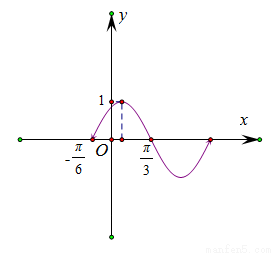
函数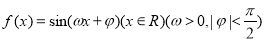 的部分图象如图所示,如果
的部分图象如图所示,如果 ,
,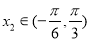 ,且
,且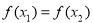 ,则
,则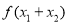 等于( )
等于( )
A.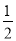 B.
B.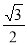 C.
C.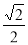 D.
D.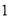
查看答案和解析>>
科目:高中数学 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试理科数学试卷(解析版) 题型:解答题
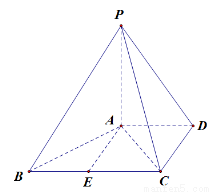
(本小题满分12分)如图,已知四棱锥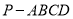 中,
中,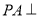 平面
平面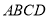 ,
,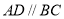 ,
,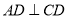 ,且
,且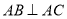 ,
,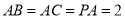 ,
,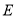 是
是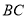 的中点.
的中点.
(1)求异面直线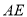 与
与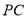 所成角;
所成角;
(2)求二面角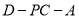 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省龙岩市非一级达标校高三上学期期末检查理科数学试卷(解析版) 题型:解答题
(本小题满分7分)选修4-4:极坐标与参数方程
在平面直角坐标系中,以坐标原点为极点,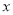 轴的正半轴为极轴建立极坐标系.已知直线
轴的正半轴为极轴建立极坐标系.已知直线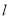 的极坐标方程为
的极坐标方程为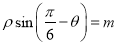 (
(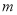 为常数),圆
为常数),圆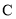 的参数方程为
的参数方程为 (
(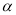 为参数).
为参数).
(1)求直线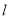 的直角坐标方程和圆
的直角坐标方程和圆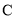 的普通方程;
的普通方程;
(2)若圆心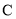 关于直线
关于直线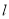 的对称点亦在圆上,求实数
的对称点亦在圆上,求实数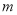 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com