Question

设函数f（x）=x³-6x²+2．
（1）当x∈[-a，a]（a＞0）时，求f（x）的最大值；
（2）设g（x）=|f（x）-k|（x∈[0，6]），用?（k）表示g（x）的最大值，求?（k）的解析式、?（k）的最小值及相应的k的值．

Answer 1

分析：（1）求出f′（x）=0时x的值，然后分区间讨论函数的增减性得到函数的极大值点为0，然后讨论a的范围得到f（x）的最大值；
（2）根据（1）求出f（x）的值域为[-30，2]，然后求出f（x）-k的值域，最大大于最小得到关于k的不等式，求出k的范围，讨论k的范围来取函数g（x）的最大值即?（k），从而得到?（k）即k的值．

解答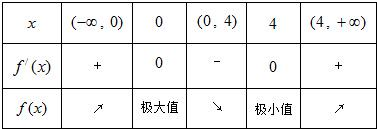：解：（1）解f′（x）=3x²-12x=0得x=0或x=4．
由f（x）=x³-6x²+2=f（0）得x=0或x=6，
所以f（x）的最大值M=

2，0＜a≤6 f(a)，a＞6

．


（2）由（1）知f（x）在x∈[0，6]的值域是[f（4），f（6）]或[f（4），f（0）]，即[-30，2]，
所以f（x）-k在x∈[0，6]的值域是[-30-k，2-k]，由|-30-k|＞|2-k|解得k＞-14，
由|-30-k|≤|2-k|解得k≤-14，
所以?(k)=

|k+30|，k＞-14 |k-2|，k≤-14

，
从而?（k）的最小值为m=16，相应的k=-14．

点评：让学生理解函数的最值及几何意义，会利用导数研究函数的极值．