
分析 作出不等式组对应的平面区域,利用z的几何意义,结合数形结合先求出m=2x-3y-6的最值,即可得到结论.
解答  解:设m=2x-3y-6,得y=$\frac{2}{3}x$$-\frac{6+m}{3}$,
解:设m=2x-3y-6,得y=$\frac{2}{3}x$$-\frac{6+m}{3}$,
作出不等式组对应的平面区域如图(阴影部分ABC):
平移直线y=$\frac{2}{3}x$$-\frac{6+m}{3}$,由图象可知当直线y=$\frac{2}{3}x$$-\frac{6+m}{3}$,
经过点C(0,-1)时,直线y=$\frac{2}{3}x$$-\frac{6+m}{3}$的截距最小,此时z最大,得m=2x-3y-6=3-6=-3,
当直线y=$\frac{2}{3}x$$-\frac{6+m}{3}$,
经过点A时,直线y=$\frac{2}{3}x$$-\frac{6+m}{3}$的截距最大,此时z最小,
由$\left\{\begin{array}{l}{y=x+1}\\{y=2x-1}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,即A(2,3),
此时m=2x-3y-6=4-9-6=-11,
即-11≤m≤-3,
则3≤|m|≤11,
即3≤z≤11,
∴z=|2x-3y-6|的最小值是3.
故答案为:3.
点评 本题主要考查线性规划的应用,利用z的几何意义,利用数形结合是解决本题的关键.本题要注意先求出m=2x-3y-6的最值,然后结合绝对值的性质进行求解是解决本题的关键.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB=2,BC=CD=1,AB∥CD,顶点D1在底面ABCD内的射影恰为点C.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB=2,BC=CD=1,AB∥CD,顶点D1在底面ABCD内的射影恰为点C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
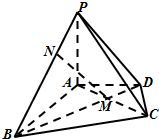 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在x<0,使得2x≥1 | B. | 任意x<0,都有2x<1 | ||
| C. | 存在x<0,使得AF∥平面BCE | D. | 存在x≥0,使得2x<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{36}{55}$ | B. | $\frac{10}{11}$ | C. | $\frac{5}{11}$ | D. | $\frac{72}{55}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com