练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．已知集合A只含有一个元素a，则下列各式中正确的是（　　）
    A．0∈AB．a∈AC．3∉AD．a=A

    分析 集合A只含有一个元素a，可得A={a}，即可判断出结论．

    解答 解：∵集合A只含有一个元素a，∴A={a}，∴a∈A．
    因此B正确．
    故选：B．

    点评 本题考查了元素与集合之间的关系及其性质，考查了推理能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    19．把一个含45°角的直角三角板BEF和一个正方形ABCD叠放在一起，使三角板的直角顶点和正方形的顶点B重合，点E，F分别在正方形的边CB，AB上，易知：AF=CE，AF⊥CE．（如图1）（不要证明）
    （1）将图1中的直角三角板BEF绕点B顺时针旋转α度（0＜α＜45），连接AF，CE，（如图2），试证明：AF=CE，AF⊥CE．
    猜想与发现：
    （2）将图2中的直角三角板BEF绕点B顺时针继续旋转，使BF落在BC边上，连接AF，CE，（如图3），点M，N分别为AF，CE的中点，连接MB，BN．
    ①MB，BN的数量关系是相等；
    ②MB，BN的位置关系是垂直．
    变式与探究：
    （3）图1中的直角三角板BEF绕点B顺时针旋转180°，点M，N分别为DF，EF的中点，连接MA，MN，（如图4），MA，MN的数量关系、位置关系又如何？为什么？

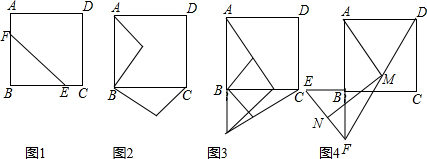
    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．设a，b，m，n∈R，且a2+b2=3，ma+nb=3，则$\sqrt{{m}^{2}{+n}^{2}}$的最小值为$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．下列说法中正确的是（　　）
    A．命题“若a＞b＞0，则$\frac{1}{a}$＜$\frac{1}{b}$”的逆命题是真命题
    B．命题p：?x∈R，x2-x+1＞0，则￢p：?x0∈R，x02-x0+1＜0
    C．“a＞1，b＞1”是“ab＞1”成立的充分条件
    D．在某项测量中，测量结果x服从正态分布N（1，σ2）（σ＞0），若x在（0，1）内取值的概率为0.4，则x在（0，2）内取值的概率为0.6

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．为第k位码元，二元码是通信中常用的码，但在通信过程中有时会发生码元错误（即码元由0变为1，或者由1变为0）．
    已知某种二元码x1x2…x7的码元满足如下校验方程组：⊕$\left\{\begin{array}{l}{{x}_{4}⊕{x}_{5}⊕{x}_{6}⊕{x}_{7}=0}\\{{x}_{2}⊕{x}_{3}⊕{x}_{6}⊕{x}_{7}=0}\\{{x}_{1}⊕{x}_{3}⊕{x}_{5}⊕{x}_{7}=0}\end{array}\right.$，其中运算⊕定义为：0⊕0=0，0⊕1=1，1⊕0=1，1⊕1=0．
    现已知一个这种二元码在通信过程中仅在第k位发生码元错误后变成了1101101，那么利用上述校验方程组可判定k等于5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．如图，某城市有一块半径为40m的半圆形绿化区域（以O为圆心，AB为直径），现对其进行改建，在AB的延长线上取点D，OD=80m，在半圆上选定一点C，改建后绿化区域由扇形区域AOC和三角形区域COD组成，其面积为Scm2．设∠AOC=xrad．
    （1）写出S关于x的函数关系式S（x），并指出x的取值范围；
    （2）试问∠AOC多大时，改建后的绿化区域面积S取得最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．二次函数y=ax2+（b-8）x-a-ab，当-3＜x＜2时，y＞0，当x＜-3或x＞2时y＜0．
    （1）求二次函数的解析式；
    （2）求y=ax2+（b-8）x-a-ab在0≤x≤1时y的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．求直线l：2x-y+3=0，关于y=-x对称的直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知变量x，y满足条件$\left\{\begin{array}{l}{0≤x≤1}\\{0≤y≤2}\\{2y-x≥1}\end{array}\right.$，
    （1）求z=2x+y的取值范围；
    （2）求$\sqrt{（x-1）^{2}+{y}^{2}}$的最小值；
    （3）求$\frac{y+1}{x+1}$的取值范围．

    查看答案和解析>>

    同步练习册答案