
| A�� | ���⡰��a��b��0����$\frac{1}{a}$��$\frac{1}{b}$������������������ | |
| B�� | ����p��?x��R��x2-x+1��0����Vp��?x0��R��x02-x0+1��0 | |
| C�� | ��a��1��b��1���ǡ�ab��1�������ij������ | |
| D�� | ��ij������У��������x������̬�ֲ�N��1����2�����ң�0������x�ڣ�0��1����ȡֵ�ĸ���Ϊ0.4����x�ڣ�0��2����ȡֵ�ĸ���Ϊ0.6 |
���� A������������Ķ�������жϣ�
B������ȫ������ķ����س���������жϣ�
C�����ݳ�������ͱ�Ҫ�����Ķ�������жϣ�
D��������̬�ֲ������ʽ����жϣ�
��� �⣺A�����⡰��a��b��0����$\frac{1}{a}$��$\frac{1}{b}$�����������ǣ�����$\frac{1}{a}$��$\frac{1}{b}$����a��b��0��Ϊ�����⣮��a��0��b��0ʱ�����������������۲���������A����
B������p��?x��R��x2-x+1��0����Vp��?x0��R��x02-x0+1��0����B����
C����a��1��b��1ʱ��ab��1������������Գ�������a��1��b��1���ǡ�ab��1�����ij����������C��ȷ��
D���߲������x������̬�ֲ�N��1����2�����ң�0�����ຯ��ͼ�����x=1�Գƣ�
��x�ڣ�0��1����ȡֵ�ĸ���Ϊ0.4����x�ڣ�0��2����ȡֵ�ĸ���Ϊ0.4��2=0.8����D����
��ѡ��C��
���� ������Ҫ�������������жϣ��漰֪ʶ��϶࣬�ۺ��Խ�ǿ�����ѶȲ���


 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
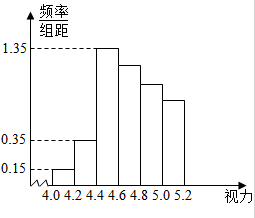 ijѧУ�о���ѧϰС��Ը�У����ѧ������������е��飬�ڸ�����ȫ��1000��ѧ���������ȡ��100��ѧ�������������õ���ͼֱ��ͼ��
ijѧУ�о���ѧϰС��Ը�У����ѧ������������е��飬�ڸ�����ȫ��1000��ѧ���������ȡ��100��ѧ�������������õ���ͼֱ��ͼ��| �Ƿ���� | 1��50 | 951��1000 | �ϼ� |
| �꼶���� | |||
| ���� | 41 | 32 | 73 |
| ������ | 9 | 18 | 27 |
| �ϼ� | 50 | 50 | 100 |
| P��K2��k�� | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 1.5 | C�� | 2 | D�� | 2.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 29 | C�� | 37 | D�� | 49 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0��A | B�� | a��A | C�� | 3∉A | D�� | a=A |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|1��x��2} | B�� | {x|2��x��4} | C�� | {x|1��x��2} | D�� | {x|2��x��4} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com