
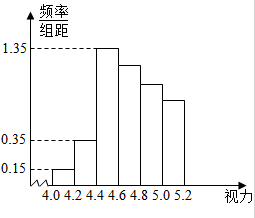
 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图直方图:
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图直方图:| 是否近视 | 1~50 | 951~1000 | 合计 |
| 年级名次 | |||
| 近视 | 41 | 32 | 73 |
| 不近视 | 9 | 18 | 27 |
| 合计 | 50 | 50 | 100 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
分析 (Ⅰ)由频率分布直方图可知:分布求得第一到第六组的频数,求得视力在5.0以的频率为1-0.08=0.82,全年级5.0以上的人数为1000×0.82=820;
(Ⅱ)求出K2,与临界值比较,K2≈4.110>3.841.由此能求出在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系.
(Ⅲ)依题意9人中年级名次在1~50名和951~1000名分别有3人和6人,X可取0、1、2、3,分别求出相应在的概率,由此能求出X的分布列和X的数学期望.
解答 解:(Ⅰ)由图可得:前三组的频率分别为:0.03,0.07,0.27,
∴第一组有3人,第二组7人,第三组有27人,
后四组频数成等差数列,
∴后四组的频数27,24,21,18,
∴所以视力在5.0以的频率为1-0.08=0.82,
所以全年级5.0以上的人数为1000×0.82=820;
(Ⅱ)K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$=$\frac{100×(41×18-32×9)^{2}}{50×50×73×27}$≈4.110>3.841.
因此,在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系;
(Ⅲ)由题意可知9人中年级名次在1-50名和951-1000名的人数分别为3人和6人,
∴X的取值为0,1,2,3,
P(X=0)=$\frac{{C}_{6}^{3}}{{C}_{9}^{3}}$=$\frac{5}{21}$,
P(X=1)=$\frac{{C}_{6}^{2}{C}_{3}^{1}}{{C}_{9}^{3}}$=$\frac{15}{28}$,
P(X=2)=$\frac{{C}_{6}^{1}{C}_{3}^{2}}{{C}_{9}^{2}}$=$\frac{3}{14}$,
P(X=3)=$\frac{{C}_{3}^{3}}{{C}_{9}^{3}}$=$\frac{1}{84}$,
X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{5}{21}$ | $\frac{15}{28}$ | $\frac{3}{14}$ | $\frac{1}{84}$ |
点评 本题考查直方图,考查独立性检验的应用,考查求X的分布列和数学期望,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,$\frac{3}{4}$] | C. | ($\frac{1}{2}$,+∞) | D. | [$\frac{3}{4}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若a>b>0,则$\frac{1}{a}$<$\frac{1}{b}$”的逆命题是真命题 | |
| B. | 命题p:?x∈R,x2-x+1>0,则¬p:?x0∈R,x02-x0+1<0 | |
| C. | “a>1,b>1”是“ab>1”成立的充分条件 | |
| D. | 在某项测量中,测量结果x服从正态分布N(1,σ2)(σ>0),若x在(0,1)内取值的概率为0.4,则x在(0,2)内取值的概率为0.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com