
分析 先求出函数f(x)的定义域为$[-4,\frac{1}{2}]$.由y=$\sqrt{2-4x}$+2$\sqrt{x+4}$两边平方可得:y2=18+4$\sqrt{-4(x+\frac{7}{4})^{2}+\frac{81}{4}}$,利用二次函数的单调性可得:y≤6,m=6.
即a+b=6.再利用“乘1法”与基本不等式的性质即可得出.
解答 解:由$\left\{\begin{array}{l}{2-4x≥0}\\{x+4≥0}\end{array}\right.$,解得$-4≤x≤\frac{1}{2}$.
∴函数f(x)的定义域为$[-4,\frac{1}{2}]$.
由y=$\sqrt{2-4x}$+2$\sqrt{x+4}$两边平方可得:y2=18+4$\sqrt{-4(x+\frac{7}{4})^{2}+\frac{81}{4}}$≤18+4×$\frac{9}{2}$=36,当且仅当x=-$\frac{7}{4}$时取等号.
∴y≤6,∴m=6.
∴a+b=6.
又a,b>0,∴$\frac{4}{a}$+$\frac{9}{b}$=$\frac{1}{6}$(a+b)$(\frac{4}{a}+\frac{9}{b})$=$\frac{1}{6}(13+\frac{4b}{a}+\frac{9a}{b})$≥$\frac{1}{6}(13+2\sqrt{\frac{4b}{a}×\frac{9a}{b}})$=$\frac{25}{6}$,当且仅当2b=3a=$\frac{36}{5}$时取等号.
∴$\frac{4}{a}$+$\frac{9}{b}$的最小值为$\frac{25}{6}$,
故答案为:$\frac{25}{6}$.
点评 本题考查了基本不等式的性质、二次函数的单调性、不等式的解法、“乘1法”,考查了推理能力与计算能力,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 6 | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
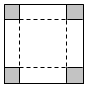 将边长为a的正方形白铁皮,在它的四角各剪去一个小正方形(剪去的四个小正方形全等)然后弯折成一只无盖的盒子,问:剪去的小正方形边长为多少时,制成的盒子容积最大?
将边长为a的正方形白铁皮,在它的四角各剪去一个小正方形(剪去的四个小正方形全等)然后弯折成一只无盖的盒子,问:剪去的小正方形边长为多少时,制成的盒子容积最大?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{10}{3}$ | C. | $\sqrt{10}$ | D. | $\frac{2\sqrt{7}+5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2$\sqrt{2}$-1,2$\sqrt{2}$-1] | B. | [-2$\sqrt{2}$-1,2$\sqrt{2}$-1) | C. | [-$\sqrt{5}$-1,$\sqrt{5}$-1] | D. | [-$\sqrt{5}$-1,$\sqrt{5}$-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com