
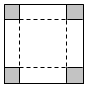
 将边长为a的正方形白铁皮,在它的四角各剪去一个小正方形(剪去的四个小正方形全等)然后弯折成一只无盖的盒子,问:剪去的小正方形边长为多少时,制成的盒子容积最大?
将边长为a的正方形白铁皮,在它的四角各剪去一个小正方形(剪去的四个小正方形全等)然后弯折成一只无盖的盒子,问:剪去的小正方形边长为多少时,制成的盒子容积最大? 分析 首先由题意建立起无盖铁盒的体积函数,变形成为(a-2x)•(a-2x)•4x,分析得到其“和”是定值,联想到利用基本不等式求最值,即可得出结论
解答 解:设剪去的小正方形的边长为x,(0<x<$\frac{a}{2}$),则无盖铁盒体积V=(a-2x)2•x.
所以:V=(a-2x)2•x=$\frac{1}{4}$(a-2x)•(a-2x)•4x≤$\frac{1}{4}•[\frac{(a-2x)+(a-2x)+4x}{3}]^{3}$=$\frac{2}{27}{a}^{3}$,
当且仅当a-2x=4x时,即x=$\frac{a}{6}$时取得最大值$\frac{2}{27}{a}^{3}$.
点评 此题主要考查利用基本不等式求最值在实际问题中的应用.前提是“一正二定三相等”,需通过变形技巧,得到“和”或“积”为定值的情形.然后应用不等式即可.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{23}{50}$ | B. | $\frac{25}{49}$ | C. | $\frac{13}{50}$ | D. | $\frac{13}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com