
分析 (1)由$\overrightarrow{a}$∥$\overrightarrow{b}$求出x的值,由$\overrightarrow{a}$⊥$\overrightarrow{c}$求出y的值,从而得出$\overrightarrow{b}$、$\overrightarrow{c}$;
(2)计算$\overrightarrow{m}$、$\overrightarrow{n}$,利用平面向量夹角的公式求出cos<$\overrightarrow{m}$,$\overrightarrow{n}$>,即得夹角的大小.
解答 解:(1)由$\overrightarrow{a}$∥$\overrightarrow{b}$得3x-4×9=0,解得x=12;
由$\overrightarrow{a}$⊥$\overrightarrow{c}$得9×4+xy=0,
解得y=-$\frac{36}{x}$=-$\frac{36}{12}$=-3;
所以$\overrightarrow{b}$=(9,12),$\overrightarrow{c}$=(4,-3);
(2)$\overrightarrow{m}$=2$\overrightarrow{a}$-$\overrightarrow{b}$=(-3,-4),
$\overrightarrow{n}$=$\overrightarrow{a}$+$\overrightarrow{c}$=(7,1);
所以$\overrightarrow{m}$•$\overrightarrow{n}$=-3×7-4×1=-25,
|$\overrightarrow{m}$|=$\sqrt{{(-3)}^{2}{+(-4)}^{2}}$=5,
|$\overrightarrow{n}$|=$\sqrt{{7}^{2}{+1}^{2}}$=5$\sqrt{2}$;
所以cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|×|\overrightarrow{n}|}$=$\frac{-25}{5×5\sqrt{2}}$=-$\frac{\sqrt{2}}{2}$,
所以向量$\overrightarrow{m}$、$\overrightarrow{n}$的夹角为$\frac{3π}{4}$.
点评 本题考查了数量积表示两个向量的夹角,平行向量与共线向量,数量积判断两个平面向量的垂直关系,其中根据“两个向量平行,坐标交叉相乘差为零,两个向量若垂直,对应相乘和为零”构造方程是解答本题的关键.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $y=\sqrt{{x^2}-1}$ | B. | y=x2 | C. | y=2x | D. | y=lnx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 6 | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{13}$ | B. | -$\frac{5}{13}$ | C. | $\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
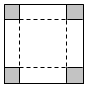 将边长为a的正方形白铁皮,在它的四角各剪去一个小正方形(剪去的四个小正方形全等)然后弯折成一只无盖的盒子,问:剪去的小正方形边长为多少时,制成的盒子容积最大?
将边长为a的正方形白铁皮,在它的四角各剪去一个小正方形(剪去的四个小正方形全等)然后弯折成一只无盖的盒子,问:剪去的小正方形边长为多少时,制成的盒子容积最大?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com