
| A. | $\frac{23}{50}$ | B. | $\frac{25}{49}$ | C. | $\frac{13}{50}$ | D. | $\frac{13}{25}$ |
分析 由等差数列的性质得$\frac{{a}_{4}}{{b}_{2}+{b}_{6}}$=$\frac{{a}_{4}}{2{b}_{4}}$=$\frac{1}{2}×\frac{{a}_{1}+{a}_{7}}{{b}_{1}+{b}_{7}}$=$\frac{1}{2}×\frac{{S}_{7}}{{T}_{7}}$,由此能求出结果.
解答 解:∵两个等差数列{an},{bn}的前n项和分别为Sn,Tn,
对任意的n∈N*,都有$\frac{{S}_{n}}{{T}_{n}}$=$\frac{2n-1}{4n-3}$,
∴$\frac{{a}_{4}}{{b}_{2}+{b}_{6}}$=$\frac{{a}_{4}}{2{b}_{4}}$=$\frac{1}{2}×\frac{{a}_{1}+{a}_{7}}{{b}_{1}+{b}_{7}}$=$\frac{1}{2}×\frac{\frac{7}{2}({a}_{1}+{a}_{7})}{\frac{7}{2}({b}_{1}+{b}_{7})}$
=$\frac{1}{2}×\frac{{S}_{7}}{{T}_{7}}$=$\frac{1}{2}×\frac{2×7-1}{4×7-3}$=$\frac{13}{50}$.
故选:C.
点评 本题考查等差数列的项的比值的求法,是中档题,解题时要认真审题,注意等差数列的性质的合理运用.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{13}$ | B. | -$\frac{5}{13}$ | C. | $\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
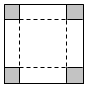 将边长为a的正方形白铁皮,在它的四角各剪去一个小正方形(剪去的四个小正方形全等)然后弯折成一只无盖的盒子,问:剪去的小正方形边长为多少时,制成的盒子容积最大?
将边长为a的正方形白铁皮,在它的四角各剪去一个小正方形(剪去的四个小正方形全等)然后弯折成一只无盖的盒子,问:剪去的小正方形边长为多少时,制成的盒子容积最大?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{(n+1)^{2}}$ | B. | $\frac{2}{n(n+1)}$ | C. | $\frac{1}{{2}^{n}-1}$ | D. | $\frac{1}{2n-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com