
分析 由已知a1=1,a2=4,a3=9,an=an-1+an-2-an-3,得到an-an-1=an-2-an-3,分别分n为奇数和偶数得到通项公式,进一步等差数列求和即可.
解答 解:由已知a1=1,a2=4,a3=9,an=an-1+an-2-an-3,得到an-an-1=an-2-an-3,
所以n为偶数时an-an-1=an-2-an-3=…=a2-a1=3,an=an-an-1+an-1-an-2+…+a2-a1+a1=$3×\frac{n}{2}+5×(\frac{n}{2}-1)$+1=4n-4,
n为奇数时an-an-1=an-2-an-3=…=a3-a2=5,an=an-an-1+an-1-an-2+…+a2-a1+a1=$3×\frac{n-1}{2}+5×\frac{n-1}{2}$+1=4n-3,
所以S2n=$4n+\frac{n(n-1)×8}{2}+n×1+\frac{n(n-1)×8}{2}$=8n2-3n
故答案为:8n2-3n.
点评 本题考查了数列求和,关键是从递推关系发现n为奇数和偶数时的通项公式,从而转化为等差数列求和.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{13}$ | B. | -$\frac{5}{13}$ | C. | $\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{2}$ | B. | $\frac{5}{2}$ | C. | -$\frac{5}{2}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
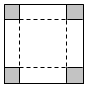 将边长为a的正方形白铁皮,在它的四角各剪去一个小正方形(剪去的四个小正方形全等)然后弯折成一只无盖的盒子,问:剪去的小正方形边长为多少时,制成的盒子容积最大?
将边长为a的正方形白铁皮,在它的四角各剪去一个小正方形(剪去的四个小正方形全等)然后弯折成一只无盖的盒子,问:剪去的小正方形边长为多少时,制成的盒子容积最大?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com