
分析 (1)由已知,得到$\overrightarrow{OA}$与$\overrightarrow{OB}$的坐标,然后根据数量积求夹角;
(2)由$\overrightarrow{OC}$与$\overrightarrow{OA}$垂直,得到数量积为0,得到点C的坐标的方程解之;
(3)根据|$\overrightarrow{OC}$|=1,结合|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$|的几何意义求最值.
解答 解:因为在平面直角坐标系中,O为坐标原点,A(1,1),B(2,0),所以$\overrightarrow{OA}=(1,1),\overrightarrow{OB}=(2,0)$,
所以(1)$\overrightarrow{OA}$与$\overrightarrow{OB}$夹角的余弦值为$\frac{\overrightarrow{OA}•\overrightarrow{OB}}{|\overrightarrow{OA}||\overrightarrow{OB|}}=\frac{2}{2\sqrt{2}}=\frac{\sqrt{2}}{2}$,所以夹角为45°;
(2)设$\overrightarrow{OC}$=(x,y).因为$\overrightarrow{OC}$与$\overrightarrow{OA}$垂直,又|$\overrightarrow{OC}$|=1.
所以$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=1}\\{x+y=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{\sqrt{2}}{2}}\\{y=\frac{\sqrt{2}}{2}}\end{array}\right.$,或$\left\{\begin{array}{l}{x=-\frac{\sqrt{2}}{2}}\\{y=-\frac{\sqrt{2}}{2}}\end{array}\right.$,所以C($\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}$),或C($-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}$).
(3)由以上得到$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=(3+x,1+y),|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$|2=(x+3)2+(y+1)2,又x2+y2=1,所以|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$|的最大值为$\sqrt{10}+1$,最小值为$\sqrt{10}-1$.
点评 本题考查了平面向量的运算,采用了坐标化的方法,使问题代数化.属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{2}$ | B. | $\frac{5}{2}$ | C. | -$\frac{5}{2}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
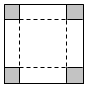 将边长为a的正方形白铁皮,在它的四角各剪去一个小正方形(剪去的四个小正方形全等)然后弯折成一只无盖的盒子,问:剪去的小正方形边长为多少时,制成的盒子容积最大?
将边长为a的正方形白铁皮,在它的四角各剪去一个小正方形(剪去的四个小正方形全等)然后弯折成一只无盖的盒子,问:剪去的小正方形边长为多少时,制成的盒子容积最大?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{(n+1)^{2}}$ | B. | $\frac{2}{n(n+1)}$ | C. | $\frac{1}{{2}^{n}-1}$ | D. | $\frac{1}{2n-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com