
分析 通过共线向量基本定理即可判断.
解答 解:若$\overrightarrow{b}$=$\overrightarrow{0}$,则$\overrightarrow{a}$与$\overrightarrow{c}$的关系为共线或不共线,
若$\overrightarrow{b}$≠$\overrightarrow{0}$,则$\overrightarrow{a}$=λ$\overrightarrow{b}$,$\overrightarrow{b}$=μ$\overrightarrow{c}$,则$\overrightarrow{a}$=λμ$\overrightarrow{c}$,则$\overrightarrow{a}$与$\overrightarrow{c}$共线,
综上所述:则$\overrightarrow{a}$与$\overrightarrow{c}$的关系是共线或不共线,
故答案为:③
点评 本题考查了共线向量得定义与性质,找出反例是判断的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
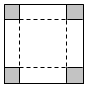 将边长为a的正方形白铁皮,在它的四角各剪去一个小正方形(剪去的四个小正方形全等)然后弯折成一只无盖的盒子,问:剪去的小正方形边长为多少时,制成的盒子容积最大?
将边长为a的正方形白铁皮,在它的四角各剪去一个小正方形(剪去的四个小正方形全等)然后弯折成一只无盖的盒子,问:剪去的小正方形边长为多少时,制成的盒子容积最大?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{4\sqrt{3}}{3}$)∪($\frac{4\sqrt{3}}{3}$,+∞) | B. | (-∞,-2)∪(2,+∞) | C. | (-∞,2$\sqrt{3}$)∪(2$\sqrt{3}$,+∞) | D. | (-∞,-4$\sqrt{3}$)∪(4$\sqrt{3}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com