
分析 求出圆x2+y2+4y-21=0的圆心、半径,当直线l的斜率不存在时,直线方程为x=-3,成立;当直线l的斜率存在时,设直线l:y=k(x+3)-3,求出圆心(0,-2)到直线y=k(x+3)-3的距离,由过点M(-3,-3)的直线l被圆x2+y2+4y-21=0所截得的弦长为8,利用勾股定理能求出直线l的方程.
解答 解:圆x2+y2+4y-21=0的圆心为(0,-2),半径r=$\frac{1}{2}\sqrt{16+84}$=5,
当直线l的斜率不存在时,直线方程为x=-3,
联立$\left\{\begin{array}{l}{x=-3}\\{{x}^{2}+{y}^{2}+4y-21=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-3}\\{y=-6}\end{array}\right.$,
∴直线l:x=-3被圆x2+y2+4y-21=0所截得的弦长为8,成立;
当直线l的斜率存在时,设直线l:y=k(x+3)-3,
圆心(0,-2)到直线y=k(x+3)-3的距离d=$\frac{|0+2+3k-3|}{\sqrt{{k}^{2}+1}}$=$\frac{|3k-1|}{\sqrt{{k}^{2}+1}}$,
∵过点M(-3,-3)的直线l被圆x2+y2+4y-21=0所截得的弦长为8,
∴由勾股定理得:${r}^{2}={d}^{2}+(\frac{8}{2})^{2}$,
即25=$\frac{(3k-1)^{2}}{{k}^{2}+1}$+16,解得k=-$\frac{4}{3}$,
∴直线l:$y=-\frac{4}{3}(x+3)-3$,整理,得:4x+3y+21=0.
综上直线l的方程为:4x+3y+21=0或x=-3.
故答案为:4x+3y+21=0或x=-3.
点评 本题考查直线方程的求法,是中档题,解题时要认真审题,注意圆的性质、点到直线的距离公式的合理运用.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:解答题
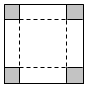 将边长为a的正方形白铁皮,在它的四角各剪去一个小正方形(剪去的四个小正方形全等)然后弯折成一只无盖的盒子,问:剪去的小正方形边长为多少时,制成的盒子容积最大?
将边长为a的正方形白铁皮,在它的四角各剪去一个小正方形(剪去的四个小正方形全等)然后弯折成一只无盖的盒子,问:剪去的小正方形边长为多少时,制成的盒子容积最大?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2$\sqrt{2}$-1,2$\sqrt{2}$-1] | B. | [-2$\sqrt{2}$-1,2$\sqrt{2}$-1) | C. | [-$\sqrt{5}$-1,$\sqrt{5}$-1] | D. | [-$\sqrt{5}$-1,$\sqrt{5}$-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{4\sqrt{3}}{3}$)∪($\frac{4\sqrt{3}}{3}$,+∞) | B. | (-∞,-2)∪(2,+∞) | C. | (-∞,2$\sqrt{3}$)∪(2$\sqrt{3}$,+∞) | D. | (-∞,-4$\sqrt{3}$)∪(4$\sqrt{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com