
| A. | 6π | B. | 8π | C. | 12π | D. | 16π |
分析 设与CD1的另一个交点为F,连结EF,DF,得BCEF是矩形,则三棱柱ABE-DCF是球O的内接直三棱柱,求出球O的半径,即可求出球O表面积.
解答 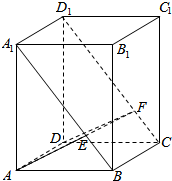 解:设球O与CD1的另一个交点为F,连结EF,DF,可得BCEF是矩形,
解:设球O与CD1的另一个交点为F,连结EF,DF,可得BCEF是矩形,
则三棱柱ABE-DCF是球O的内接直三棱柱,
∵正方体ABCD-A1B1C1D1中,AB=2,AE⊥BA1,
∴AE=BE=$\sqrt{2}$,
∴球O的半径R=$\frac{\sqrt{{\sqrt{2}}^{2}+{\sqrt{2}}^{2}+{2}^{2}}}{2}$=$\sqrt{2}$,
∴球O表面积为:4πR2=4π•($\sqrt{2}$)2=8.
故选:B.
点评 本题主要考查球的表面积公式,以及球内接三棱柱的关系,考查空间想象能力以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
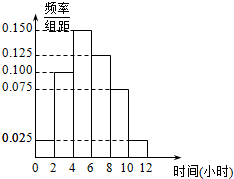 某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,1,-7) | B. | (5,13,-3) | C. | (-3,1,5) | D. | (5,3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n⊥β,且α⊥β,则m∥n | B. | 若α∥β,m?α,n?β,则m∥n | ||
| C. | 若m⊥α,n⊥β,m⊥n,则α⊥β | D. | 若m⊥n,m?α,n?β,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com