
 某学校为调查来自南方和北方的同龄大学生的身高差异,从2014级的年龄在17~19岁之间的大学生中随机抽取了自南方和北方的大学生各10名,测量他们的身高,量出的身高如下(单位:cm)
某学校为调查来自南方和北方的同龄大学生的身高差异,从2014级的年龄在17~19岁之间的大学生中随机抽取了自南方和北方的大学生各10名,测量他们的身高,量出的身高如下(单位:cm)分析 (1)根据所提供数据,将前两位数作为茎,最后一个数作为叶,即可得到茎叶图,从而可得统计结论;
(2)根据流程图的含义可知S表示10位南方大学生身高的方差,是描述身高离散程度的量,根据方差公式解之可得S.
解答 (本题满分为12分)
解:(1)茎叶图如图所示: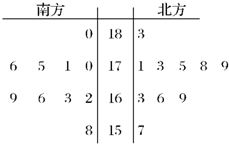
统计结论:(给出下述四个供参考,考生只要答对其中两个即可,给出其他合理的答案也可)
①北方大学生的平均身高大于南方大学生的平均身高.
②南方大学生身高比北方大学生的身高更整齐.
③南方大学生的身高的中位数为169.5 cm,北方大学生的身高的中位数是172 cm.
④南方大学生的高度基本上是对称的,而且大多数集中在均值附近,北方大学生的高度分布较为分散.…(6分)
(2)$\overline{x}$=169,S=42.6,
S表示10位南方大学生身高的方差,是描述身高离散程度的量,
S值越小,表示身高越整齐,S值越大,表示身高参差不齐.…(12分)
点评 本题主要考查了茎叶图和算法流程图,以及平均数、中位数和方差的度量,同时考查了识图能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 直线 | B. | 圆 | C. | 线段 | D. | 射线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 5吨 | 0.9万元 | 0.3万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
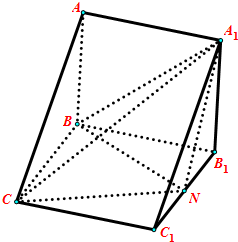 在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.N为B1C1中点.
在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.N为B1C1中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{225}$ | B. | $\frac{1}{300}$ | C. | $\frac{1}{450}$ | D. | 以上全不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x3 | B. | y=$\frac{1}{x-1}$ | C. | y=log2$\frac{1}{x}$ | D. | y=-tanx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{10}$ | B. | $\frac{19}{21}$ | C. | $\frac{10}{11}$ | D. | $\frac{11}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
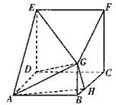 在多面体ABCDEFG中,四边形ABCD与CDEF均为边长为4的正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH.
在多面体ABCDEFG中,四边形ABCD与CDEF均为边长为4的正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com